
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 是
是![]() 的弦,且
的弦,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的度数是( )
的度数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
连接OE、FB.在△EFO中,由等边对等角得到∠FEO的度数,证明△EFO≌△EBO,得到∠BEO=∠FEO,从而得到∠FEB的度数.在△EFB中,根据等边对等角和三角形内角和定理得出∠EFB的度数,进而得到∠OFB的度数.在△OFB中,根据等边对等角得出∠OBF的度数,根据圆周角定理即可得到∠AOF的度数.
连接OE、FB.
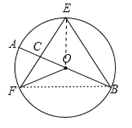
∵OF=OE,∴∠FEO=∠EFO=35°.
在△EFO和△EBO中,∵EF=BE,OE=OE,OF=OB,
∴△EFO≌△EBO,∴∠BEO=∠FEO=35°,∴∠FEB=70°.
∵EF=EB,∴∠EFB=∠EBF=(180°-70°)÷2=55°,∴∠OFB=∠EFB-∠EFO=55° -35°=20°.
∵OF=OB,∴∠OBF=∠OFB=20°,∴∠AOF=2∠OBF=40°.
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
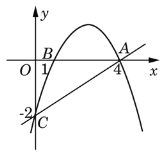
【题目】如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
(1)求出抛物线的解析式;
(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
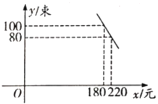
【题目】女本柔弱,为母则刚,说的是母亲对子女无私的爱,母爱伟大,值此母亲节来临之际,某花店推出一款康乃馨花束,经过近几年的市场调研发现,该花束在母亲节的销售量![]() (束)与销售单价
(束)与销售单价![]() (元)之间满足如图所示的一次函数关系,已知该花束的成本是每束100元.
(元)之间满足如图所示的一次函数关系,已知该花束的成本是每束100元.
(1)求出![]() 关于
关于![]() 的函数关系式(不要求写
的函数关系式(不要求写![]() 的取值范围);
的取值范围);
(2)设该花束在母亲节盈利为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式:并求出当售价定为多少元时,利润最大?最大值是多少?
的函数关系式:并求出当售价定为多少元时,利润最大?最大值是多少?
(3)花店开拓新的进货渠道,以降低成本.预计在今后的销售中,母亲节期间该花束的销售量与销售单价仍存在(1)中的关系.若想实现销售单价为200元,且销售利润不低于9900元的销售目标,该花束每束的成本应不超过多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的日益提高,人们越来越喜欢过节,节日的仪式感日渐浓烈.某校举行了“女神节暖心特别行动”,从中随机调査了部分同学的暖心行动,并将其分为A,B,C,D四种类型(分别对应送服务、送鲜花、送红包、送话语).现根据调查的数据绘制成如下的条形统计图和扇形统计图.
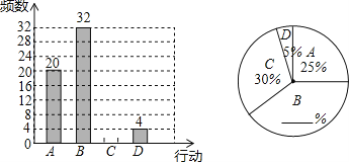
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该校共抽查了多少名同学的暖心行动?
(2)补全条形统计图和扇形统计图;
(3)若该校共有2400名同学,请估计该校进行送鲜花行动的同学约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
观察猜想
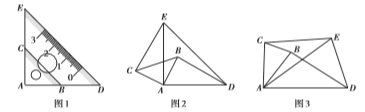
如图1,有公共直角顶点![]() 的两个不全等的等腰直角三角尺叠放在一起,点
的两个不全等的等腰直角三角尺叠放在一起,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上.
上.
(1)在图1中,你发现线段![]() ,
,![]() 的数量关系是___________,直线
的数量关系是___________,直线![]() ,
,![]() 的位置关系是________.
的位置关系是________.
操作发现
(2)将图1中的![]() 绕点
绕点![]() 逆时针旋转一个锐角得到图2,这时(1)中的两个结论是否成立?作出判断并说明理由;
逆时针旋转一个锐角得到图2,这时(1)中的两个结论是否成立?作出判断并说明理由;
拓广探索
(3)如图3,若只把“有公共直角顶点![]() 的两个不全等的等腰直角三角尺”改为“有公共顶角为
的两个不全等的等腰直角三角尺”改为“有公共顶角为![]() (锐角)的两个不全等等腰三角形”,
(锐角)的两个不全等等腰三角形”,![]() 绕点
绕点![]() 逆时针旋转任意一个锐角,这时(1)中的两个结论仍然成立吗?作出判断,不必说明理由.
逆时针旋转任意一个锐角,这时(1)中的两个结论仍然成立吗?作出判断,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:问题情境:在一次综合实践活动课上,同学们以菱形为对象,研究菱形旋转中的问题:已知,在菱形![]() 中,
中,![]() 为对角线,
为对角线,![]() ,
,![]() ,将菱形
,将菱形![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() (单位
(单位![]() ).旋转后的菱形为
).旋转后的菱形为![]() .在旋转探究活动中提出下列问题,请你帮他们解决.
.在旋转探究活动中提出下列问题,请你帮他们解决.
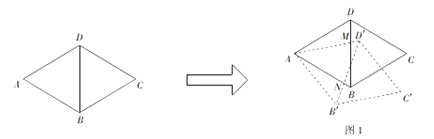
(1)如图1,若旋转角![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .请说明线段
.请说明线段![]() 与
与![]() 的数量关系;
的数量关系;
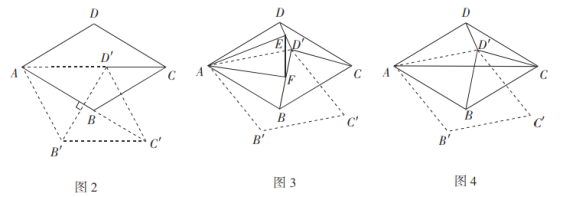
(2)如图2,连接![]() ,菱形
,菱形![]() 旋转的过程中,当
旋转的过程中,当![]() 与
与![]() 互相垂直时,
互相垂直时,![]() 的长为______;
的长为______;
(3)如图3,若旋转角为![]() 时,分别连接
时,分别连接![]() ,
,![]() ,过点
,过点![]() 分别作
分别作![]() ,
,![]() ,连接
,连接![]() ,菱形
,菱形![]() 旋转的过程中,发现在
旋转的过程中,发现在![]() 中存在长度不变的线段
中存在长度不变的线段![]() ,请求出
,请求出![]() 长度;
长度;
操作探究:(4)如图4,在(3)的条件下,请判断以![]() ,
,![]() ,
,![]() 三条线段长度为边的三角形是什么特殊三角形,并说明理由.
三条线段长度为边的三角形是什么特殊三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com