
����Ŀ���ۺ���ʵ��
�۲����
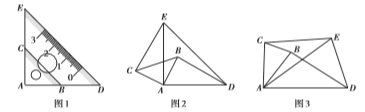
��ͼ1���й���ֱ�Ƕ���![]() ��������ȫ�ȵĵ���ֱ�����dzߵ�����һ�𣬵�
��������ȫ�ȵĵ���ֱ�����dzߵ�����һ�𣬵�![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ��.
��.
��1����ͼ1�У��㷢���߶�![]() ��
��![]() ��������ϵ��___________��ֱ��
��������ϵ��___________��ֱ��![]() ��
��![]() ��λ�ù�ϵ��________.
��λ�ù�ϵ��________.
��������
��2����ͼ1�е�![]() �Ƶ�
�Ƶ�![]() ��ʱ����תһ����ǵõ�ͼ2����ʱ��1���е����������Ƿ�����������жϲ�˵�����ɣ�
��ʱ����תһ����ǵõ�ͼ2����ʱ��1���е����������Ƿ�����������жϲ�˵�����ɣ�
�ع�̽��
��3����ͼ3����ֻ�����й���ֱ�Ƕ���![]() ��������ȫ�ȵĵ���ֱ�����dz�����Ϊ���й�������Ϊ
��������ȫ�ȵĵ���ֱ�����dz�����Ϊ���й�������Ϊ![]() ����ǣ���������ȫ�ȵ�������������
����ǣ���������ȫ�ȵ�������������![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת����һ����ǣ���ʱ��1���е�����������Ȼ�����������жϣ�����˵������.
��ʱ����ת����һ����ǣ���ʱ��1���е�����������Ȼ�����������жϣ�����˵������.
���𰸡���1��![]() ��
��![]() ����2����ͼ1�е�
����2����ͼ1�е�![]() �Ƶ�
�Ƶ�![]() ��ʱ����תһ�����ʱ���������۳���.���ɼ���������3������
��ʱ����תһ�����ʱ���������۳���.���ɼ���������3������![]() ����������
����������![]() ������.
������.
��������
��1�����ݡ�ABC�͡�ADE�ǵ���ֱ�������Σ��õ�AB=AC��AD=AE����A=90�㣬���ɵó����ۣ�
��2������ת�����ʵõ���DAB=��EAC������SAS֤����ABD�ա�ACE������ȫ�������εĶ�Ӧ����ȵó�BD=CE���ӳ�DB����CE�ڵ�F����AE�ڵ�O����ȫ�������ζ�Ӧ����ȵõ���ADB=��AEC�������������ڽǺͶ����ͶԶ�����ȣ��õ���OFE=��OAD=90�㣬���ɵó����ۣ�
��3�����ƣ�2���ɵ�BD=CE������BD��CE��������
��1���ߡ�ABC�͡�ADE�ǵ���ֱ�������Σ���AB=AC��AD=AE����A=90�㣬��BD=CE��BD��CE��
�ʴ�Ϊ��BD=CE��BD��CE��
��2����ͼ1�еġ�ABC�Ƶ�A��ʱ����תһ�����ʱ���������۳������������£�
����ת�ã���DAB=��EAC��
�֡�AB=AC��AD=AE��
���ABD�ա�ACE��SAS����
��BD=CE��
��ͼ���ӳ�DB����CE�ڵ�F����AE�ڵ�O��
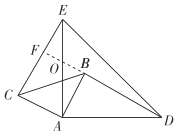
�ߡ�ABD�ա�ACE��
���ADB=��AEC��
�ߡ�AOD=��EOF��
���OFE=��OAD��
�ߡ�OAD=90�㣬
���DFE=90�㣬��BD��CE��
��3������BD=CE����������BD��CE���������������£�
����ת�ã���DAE=��BAC��
���DAB=��EAC��
�֡�AB=AC��AD=AE��
���ABD�ա�ACE��SAS����
��BD=CE��
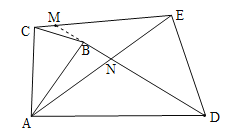
�ӳ�DB��CE��M��BD��AE���ڵ�N��
�ߡ�ABD�ա�ACE�����MEA=��BDA��
�ߡ�ENM=��DNA�����EMN=��EAD��
�ߡ�EAD��90�㣬���EMN��90�㣬��BD��CE��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������������1������1�������n��������Щ�����ɫ�����������
��1���Ӵ����������һ����¼����ɫ��Ȼ��Żأ����ȣ������ظ���ʵ�飬�������������Ƶ���ȶ���0.2����n��ֵ��
��2����![]() ��С��������������һ����Żأ�������һ��������״ͼ����С����������н�������������������ͬ��ɫ��ĸ��ʣ�
��С��������������һ����Żأ�������һ��������״ͼ����С����������н�������������������ͬ��ɫ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ���ACB��90������A�ڷ���������y����![]() ��ͼ���ϣ���B��C���ڷ���������y����
��ͼ���ϣ���B��C���ڷ���������y����![]() ��ͼ���ϣ�AB��x�ᣬ���A������Ϊ�� ��
��ͼ���ϣ�AB��x�ᣬ���A������Ϊ�� ��

A.(��![]() ��2
��2![]() )B.(��
)B.(��![]() ��
��![]() )C.(��
)C.(��![]() ��
��![]() )D.(��2
)D.(��2![]() ��
��![]() )
)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y��ax2��![]() x+c��ֱ��y��
x+c��ֱ��y��![]() x+
x+![]() ����A��B���㣬��֪��B�ĺ�������4��ֱ��y��
����A��B���㣬��֪��B�ĺ�������4��ֱ��y��![]() x+
x+![]() ��x��y��Ľ���ֱ�ΪA��C����P����������һ���㣮
��x��y��Ľ���ֱ�ΪA��C����P����������һ���㣮
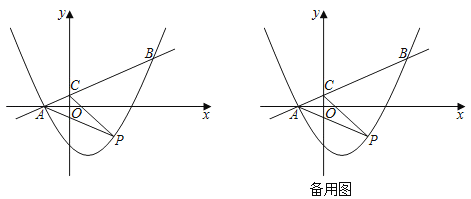
��1���������ߵĽ���ʽ��
��2������P��ֱ��y��![]() x+
x+![]() �·������PAC����������
�·������PAC����������
��3����M�������߶Գ����ϵ�һ�㣬�Ե�A��B��P��MΪ������ı����ܷ��Ϊƽ���ı��Σ����ܣ������P�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() ��
��![]() ���ң���
���ң���![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ����
����![]() ����
����![]() �Ķ����ǣ� ��
�Ķ����ǣ� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij�����꼶ѧ����˯������������ȡ�˸������꼶ѧ������ѧ�����е���.��֪D���ѧ����15�ˣ����ó������õ����ݻ�����ʾ��ͳ��ͼ��.
һ��ѧ��˯��������������λ��Сʱ��
��� | ˯��ʱ�� |
|
|
|
|
|
|
|
|
|
|
����ѧ��˯�����ͳ��ͼ
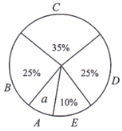
����ͼ���ṩ����Ϣ���ش��������⣺
��1�����������꼶ѧ��˯�����ͳ��ͼ���е�a��ֵ��a��Ӧ�����ε�Բ�ĽǶ�����
��2�����˯��ʱ��x��ʱ�����㣺![]() ����˯��ʱ��ϸ�.��֪�������꼶ѧ����3250�ˣ��Թ��Ƹ������꼶ѧ��˯��ʱ��ϸ�Ĺ��ж����ˣ�
����˯��ʱ��ϸ�.��֪�������꼶ѧ����3250�ˣ��Թ��Ƹ������꼶ѧ��˯��ʱ��ϸ�Ĺ��ж����ˣ�
��3������������ѧ��˯������������Сֵ����C����У�ȡ![]() ����B��C��D����ѧ����ƽ��˯��ʱ����Ϊ���꼶ѧ����˯��ʱ�������.����������꼶ѧ����ƽ��˯��ʱ��.
����B��C��D����ѧ����ƽ��˯��ʱ����Ϊ���꼶ѧ����˯��ʱ�������.����������꼶ѧ����ƽ��˯��ʱ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���γ��Ӽ�ʻ���ҵأ������ҵغؼأ��ٶ���ԭ����1.5��������tСʱ��һ������ͬʱ�Ӽ�ʻ���ҵأ������ҵغ�ֹͣ������ͬʱ������������ʻ����γ���ʻ��ʱ��Ϊx��h�����������صľ���Ϊy��km����������ʻ������y��x֮��ĺ���ͼ����ͼ��
��1����γ����ҵط��ؼ�ʱ���ٶȺ�t��ֵ��
��2����γ����ҵط��ؼ�ʱy��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3��ֱ��д���γ����ҵط��ؼ�ʱ�����������ʱ�䣮
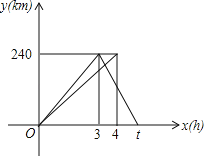
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ����С��A����·BD�ľ��룬���ڵ�B����á�ABD��37�㣬����BD����ǰ��150m�����C����á�ACD��45�㣬��С��A����·BD�ľ��룮(�ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75)
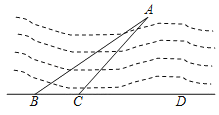
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ��ֱ�߹���(0��4)������������y��![]() x2����A��B���㣬���е�A�ĺ������ǣ�2.
x2����A��B���㣬���е�A�ĺ������ǣ�2.
(1)������ֱ�ߵĽ���ʽ����B�����ꣻ
(2)��x�����Ƿ���ڵ�C��ʹ�á�ABC��ֱ�������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ�
(3)���߶�AB��һ��P����PM��x�ᣬ���������ڵ�M����M�ڵ�һ���ޣ���N(0��1)������M�ĺ�����Ϊ��ֵʱ��MN��3MP�ij���������ֵ�Ƕ��٣�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com