
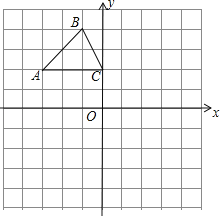
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(﹣3,2),B(﹣1,4),C(0,2).
(1)请画出△ABC关于点O的对称图形△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2并求出在旋转过程中点B所经过的圆弧长.
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:
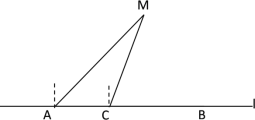
【题目】如图,在东西方向的海岸线l上有长为300米的码头AB,在码头的最西端A处测得轮船M在它的北偏东45°方向上;同一时刻,在A点正东方向距离100米的C处测得轮船M在北偏东22°方向上.
(1)求轮船M到海岸线l的距离;(结果精确到0.01米)
(2)如果轮船M沿着南偏东30°的方向航行,那么该轮船能否行至码头AB靠岸?请说明理由.
(参考数据:sin22°≈0.375,cos22°≈0.927,tan22°≈0.404,![]() ≈1.732.)
≈1.732.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加学校秋季运动会,有以下 5 个项目可供选择:径赛项目:100m、200m、1000m(分别用 A1、A2、A3 表示);田赛项目:跳远,跳高(分别用 T1、T2 表示).
(1)该同学从 5 个项目中任选一个,恰好是田赛项目的概率 P 为 ;
(2)该同学从 5 个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率 P1,利用列表法或树状图加以说明;
(3)该同学从 5 个项目中任选两个,则两个项目都是径赛项目的概率 P2 为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
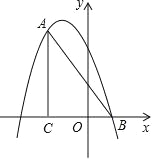
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)求点A的坐标;
(2)求抛物线的解析式;
(3)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:

根据以上数据,估算袋中的白棋子数量为( )
A. 60枚B. 50枚C. 40枚D. 30枚
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
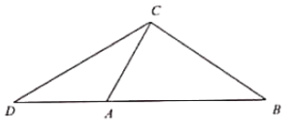
【题目】如图,已知在![]() 中,∠ACB=90°,
中,∠ACB=90°,![]() ,延长边BA至点D,使AD=AC,联结CD.
,延长边BA至点D,使AD=AC,联结CD.
(1)求∠D的正切值;
(2)取边AC的中点E,联结BE并延长交边CD于点F,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年第18号台风“米娜”于9月29日早晨5点整,由位于台湾省周边的B岛东南方约980千米的西北太平洋洋面上(A点)生成,向西北方向移动.并于9月30日20时30分到达B岛后风力增强且转向,一路向北于24小时后在浙江省舟山市登陆.“米娜”在登录后风力减弱且再一次转向,以每小时20千米的速度向北偏东30的方向移动,距台风中心170千米的范围内是受台风影响的区域.已知上海位于舟山市北偏西7方向,且距舟山市250千米.
(1)台风中心从生成点(A点)到达B岛的速度是每小时多少千米?
(2)10月2日上海受到“米娜”影响,那么上海遭受这次台风影响的时间有多长?(结果保留整数,参考数据:![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() .)
.)
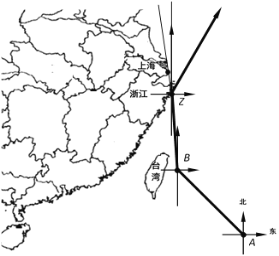
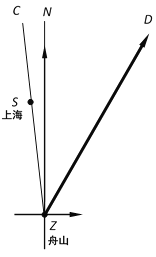
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张扑克牌的点数分别是2、3、4、8,将它们洗匀后背面朝上放在桌面上.
(1)从中随机抽取一张牌,求这张牌的点数是偶数的概率;
(2)从中先随机抽取一张牌,接着再抽取一张牌,求这两张牌的点数都是偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com