
【题目】已知抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,与
,与![]() 轴相交于
轴相交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 右侧),与
右侧),与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线的解析式和![]() ,
,![]() 两点的坐标;
两点的坐标;
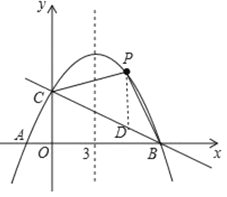
(2)如图,若点![]() 是抛物线上
是抛物线上![]() 、
、![]() 两点之间的一个动点(不与
两点之间的一个动点(不与![]() 、
、![]() 重合),是否存在点
重合),是否存在点![]() ,使四边形
,使四边形![]() 的面积最大?若存在,求点
的面积最大?若存在,求点![]() 的坐标及四边形
的坐标及四边形![]() 面积的最大值;若不存在,请说明理由.
面积的最大值;若不存在,请说明理由.
【答案】(1)抛物线的解析式为:![]() ;点
;点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)存在点
;(2)存在点![]() ,使四边形
,使四边形![]() 的面积最大;点
的面积最大;点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 面积的最大值为32.
面积的最大值为32.
【解析】
(1)根据对称轴公式可以求出a,从而可得抛物线解析式,再解出抛物线解析式y=0是的两个根,即可得到A,B的坐标;
(2)根据解析式可求出C点坐标,然后设直线![]() 的解析式为
的解析式为![]() ,从而可求该解析式方程,假设存在点
,从而可求该解析式方程,假设存在点![]() ,使四边形
,使四边形![]() 的面积最大,设点
的面积最大,设点![]() 的坐标为
的坐标为![]() ,然后过点
,然后过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,从而可求答案.
,从而可求答案.
解:(1)∵抛物线的对称轴是直线![]() ,
,
∴ ,解得
,解得![]() ,
,
∴抛物线的解析式为:![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
答:抛物线的解析式为:![]() ;点
;点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(2)当![]() 时,
时,![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() ,
,![]() 代入
代入![]() 得
得![]() ,解得
,解得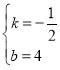 ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
假设存在点![]() ,使四边形
,使四边形![]() 的面积最大,
的面积最大,
设点![]() 的坐标为
的坐标为![]() ,
,
如图所示,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,
∴![]()
![]()
∴当![]() 时,四边形
时,四边形![]() 的面积最大,最大值是32
的面积最大,最大值是32
∵![]() ,
,
∴存在点![]() ,使得四边形
,使得四边形![]() 的面积最大.
的面积最大.
答:存在点![]() ,使四边形
,使四边形![]() 的面积最大;点
的面积最大;点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 面积的最大值为32.
面积的最大值为32.


科目:初中数学 来源: 题型:
【题目】在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证 EG=CG且EG⊥CG.
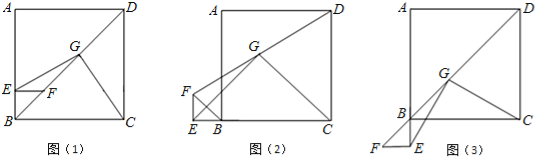
(1)将△BEF绕点B逆时针旋转90°,如图(2),则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.
(2)将△BEF绕点B逆时针旋转180°,如图(3),则线段EG和CG又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
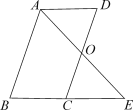
(1)求证:△AOD≌△EOC;
(2)连接AC、DE,当∠B=∠AEB=45°时,求证四边形 ACED是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
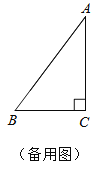
【题目】如图,在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm.动点P,Q从点A同时出发,点P沿AB向终点B运动;点Q沿AC→CB向终点B运动,速度都是1cm/s.当一个点到达终点时,另一个点同时停止运动.设点P运动的时间为t(s),在运动过程中,点P,点Q经过的路线与线段PQ围成的图形面积为S(cm2).
(1)AC=_________cm;
(2)当点P到达终点时,BQ=_______cm;
(3)①当t=5时,s=_________;
②当t=9时,s=_________;
(4)求S与t之间的函数解析式.
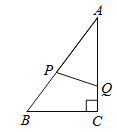
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC
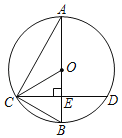
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A→B→C→M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是( )

A.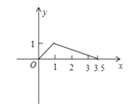 B.
B.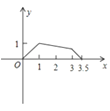 C.
C.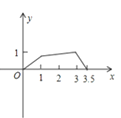 D.
D.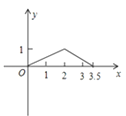
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古贤常说万物皆自然,而古希腊学者说万物皆数.同学们还记得我们最初接触的数就是“自然数”吧!在数的学习过程中,我们会对其中一些具有某种特性的自然数进行研究,我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特珠的自然数—“![]() 喜数”.
喜数”.
定义:对于一个两位自然数,如果它的个位和十位上的数字均不为零,且它正好等于其个位和十位上的数字的和的![]() 倍(
倍(![]() 为正整数),我们就说这个自然数是一个“
为正整数),我们就说这个自然数是一个“![]() 喜数”.
喜数”.
例如:24就是一个“4喜数”,因为![]()
25就不是一个“![]() 喜数”因为
喜数”因为![]()
(1)判断44和72是否是“![]() 喜数”?请说明理由;
喜数”?请说明理由;
(2)试讨论是否存在“7喜数”若存在请写出来,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型水果超市销售无锡水蜜桃,根据前段时间的销售经验,每天的售价x(元/箱)与销售量y(箱)有如表关系:
每箱售价x(元) | 68 | 67 | 66 | 65 | … | 40 |
每天销量y(箱) | 40 | 45 | 50 | 55 | … | 180 |
已知y与x之间的函数关系是一次函数.
(1)求y与x的函数解析式;
(2)水蜜桃的进价是40元/箱,若该超市每天销售水蜜桃盈利1600元,要使顾客获得实惠,每箱售价是多少元?
(3)七月份连续阴雨,销售量减少,超市决定采取降价销售,所以从7月17号开始水蜜桃销售价格在(2)的条件下,下降了m%,同时水蜜桃的进货成本下降了10%,销售量也因此比原来每天获得1600元盈利时上涨了2m%(m<100),7月份(按31天计算)降价销售后的水蜜桃销售总盈利比7月份降价销售前的销售总盈利少7120元,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com