
【题目】下面是课本中“作一个角等于已知角”的尺规作图过程.
已知:∠AOB.
求作:一个角,使它等于∠AOB.
作法:如图
(1)作射线O'A';
(2)以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
(3)以O'为圆心,OC为半径作弧C'E',交O'A'于C';
(4)以C'为圆心,CD为半径作弧,交弧C'E'于D';
(5)过点D'作射线O'B'.
则∠A'O'B'就是所求作的角.
请回答:该作图的依据是_____.
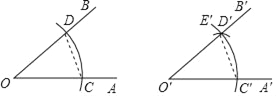
科目:初中数学 来源: 题型:
【题目】小明解方程![]() 出现了错误,解答过程如下:
出现了错误,解答过程如下:
方程两边都乘以![]() ,得
,得![]() (第一步)
(第一步)
去括号,得![]() (第二步)
(第二步)
移项,合并同类项,得![]() (第三步)
(第三步)
解得![]() (第四步)
(第四步)
![]() 原方程的解为
原方程的解为![]() (第五步)
(第五步)
(1)小明解答过程是从第_____步开始出错的,这一步正确的解答结果_____,此步的根据是_____.
(2)小明的解答过程缺少_____步骤,此方程的解为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)
(1)观察下列算式,并完成填空:
1=12
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+…+(2n-1)=______.(n是正整数)
(2)如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.
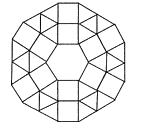
①第3层中分别含有______块正方形和______块正三角形地板砖;
②第n层中含有______块正三角形地板砖(用含n的代数式表示).
(应用)
该市打算在一个新建广场中央,采用如图样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E为长方形纸片ABCD的边CD上一点,将纸片沿AE对折,点D的对应点D′恰好在线段BE上.若AD=3,DE=1,则AB=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代有二十四节气歌,“春雨惊春清谷天,夏满芒夏暑相连.秋处露秋寒霜降,冬雪雪冬小大寒.”它是为便于记忆我国古时历法中二十四节气而编成的小诗歌,流传至今.节气指二十四时节和气候,是中国古代订立的一种用来指导农事的补充历法,是中国古代劳动人民长期经验的积累和智慧的结晶.其中第一个字“春”是指立春,为春季的开始,但在气象学上的入春日是有严格定义的,即连续5天的日平均气温稳定超过![]() 又低于
又低于![]() ,才算是进入春天,其中,5天中的第一天即为入春日.例如:2014年3月13日至18日,北京的日平均气温分别为
,才算是进入春天,其中,5天中的第一天即为入春日.例如:2014年3月13日至18日,北京的日平均气温分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,即从3月14日开始,北京日平均气温已连续5天稳定超过
,即从3月14日开始,北京日平均气温已连续5天稳定超过![]() ,达到了气象学意义上的入春标准.因此可以说2014年3月14日为北京的入春日.日平均温度是指一天24小时的平均温度.气象学上通常用一天中的2时、8时、14时、20时4个时刻的气温的平均值作为这一天的日平均气温(即4个气温相加除以4),结果保留一位小数.如表是北京顺义2017年3月28日至4月3日的气温记录及日平均气温(单位:
,达到了气象学意义上的入春标准.因此可以说2014年3月14日为北京的入春日.日平均温度是指一天24小时的平均温度.气象学上通常用一天中的2时、8时、14时、20时4个时刻的气温的平均值作为这一天的日平均气温(即4个气温相加除以4),结果保留一位小数.如表是北京顺义2017年3月28日至4月3日的气温记录及日平均气温(单位:![]() )
)
时间 | 2时 | 8时 | 14时 | 20时 | 平均气温 |
3月28日 | 6 | 8 | 13 | 11 | 9.5 |
3月29日 | 7 | 6 | 17 | 14 | a |
3月30日 | 7 | 9 | 15 | 12 | 10.8 |
3月31日 | 8 | 10 | 19 | 13 | 12.5 |
4月1日 | 8 | 7 | 18 | 15 | 12 |
4月2日 | 11 | 7 | 22 | 16 | 14 |
4月3日 | 13 | 11 | 21 | 17 | 15.5 |
根据以上材料解答下列问题:
(1)求出3月29日的日平均气温![]() ;
;
(2)采用适当的统计图将这7天的日平均气温的变化情况表示出来;
(3)请指出2017年的哪一天是北京顺义在气象学意义上的入春日.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线l过点(0,2),且与x轴平行;直线![]() 与y轴交于A点,与直线l交于B点;抛物线
与y轴交于A点,与直线l交于B点;抛物线![]() 的顶点为C.
的顶点为C.
(1)求A,B两点的坐标;
(2)求点C的坐标(用m表示);
(3)若抛物线![]() 与线段AB有公共点,求m的取值范围.
与线段AB有公共点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=﹣2x2+4x+m+1,与x轴的公共点为A,B.
(1)如果A与B重合,求m的值;
(2)横、纵坐标都是整数的点叫做整点:
①当m=﹣1时,求线段AB上整点的个数;
②若设抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,当1<n≤8时,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
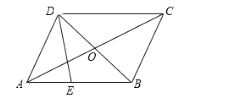
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O.E为边AB上一点,且BE = 2AE.设![]() ,
,![]() .
.
(1)填空:向量![]() ;
;
(2)如果点F是线段OC的中点,那么向量![]() ,并在图中画出向量
,并在图中画出向量![]() 在向量
在向量![]() 和
和![]() 方向上的分向量.
方向上的分向量.
注:本题结果用向量![]() 的式子表示.画图不要求写作法,但要指出所作图中表示结论的向量.
的式子表示.画图不要求写作法,但要指出所作图中表示结论的向量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com