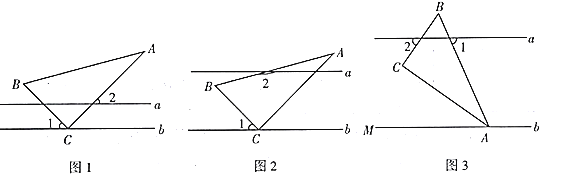
【题目】某学习小组在探究三角形全等时，发现了下面这种典型的基本图形：
如图1，已知：在
中，
，
，直线m经过点A，
直线m，
直线m，垂足分别为点D、
试猜想DE、BD、CE有怎样的数量关系，请直接写出；
组员小颖想，如果三个角不是直角，那结论是否会成立呢？如图2，将中的条件改为：在中，，D、A、E三点都在直线m上，并且有
其中
为任意锐角或钝角
如果成立，请你给出证明；若不成立，请说明理由．
数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：
如图3，F是
角平分线上的一点，且
和
均为等边三角形，D、E分别是直线m上A点左右两侧的动点
、E、A互不重合
，在运动过程中线段DE的长度始终为n，连接BD、CE，若
，试判断
的形状，并说明理由．
【答案】
，理由见解析；
结论
成立；理由见解析；
为等边三角形，理由见解析.
【解析】
（1）先利用同角的余角相等，判断出
，进而判断△ADB≌△CEA，得出BD=AE，AD=CE，即可得出结论；
（2）先利用三角形内角和及平角的性质，判断出，进而判断出△ADB≌△CEA，得出BD=AE，AD=CE，即可得出结论；
（3）由（2）得，△ADB≌△CEA，得出BD=AE，再判断出△FBD≌△FAE，得出
，进而得出
，即可得出结论．
，
理由：
，
，
，
，
，
，
，
在
和
中，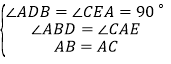
，
≌
，
，
，
，
故答案为：；
解：结论成立；
理由如下：
，
，
，
，
在
和
中，
，
≌
，
，，
；
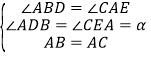为等边三角形，
理由：由得，≌，
，，
，即
，
在
和
中，
，
≌
，
，
，
，
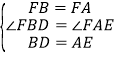为等边三角形．
故答案为：（1）DE=BD+CE，理由见解析；（2）结论DE=BD+CE成立；理由见解析；（3）△DFE为等边三角形，理由见解析.
科目：初中数学 来源： 题型：
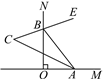
【题目】如图，∠MON＝90°，点A，B分别在射线OM，ON上运动，BE平分∠ABN，BE的反向延长线与∠BAO的平分线交于点C.
(1)当点A，B移动后，∠BAO＝45°时，∠C＝________；
(2)当点A，B移动后，∠BAO＝60°时，∠C＝________；
(3)由(1)(2)猜想∠C是否随点A，B的移动而发生变化，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】经过建设者三年的努力，贯穿四川的“遂内高速”正式通车，已知原来从遂宁到内江的公路长150km，高速公路路程比公路缩短30km，一辆小车从遂宁到内江走高速公路的平均速度可以提高到原来的1.5倍，用时比原来减少1小时，求小车原来的平均速度和走高速的平均速度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在综合与实践课上，同学们以“一个含
的直角三角尺和两条平行线”为背景开展数学活动，如图，已知两直线
且
和直角三角形
，
，
，
.
操作发现：
（1）在如图1中，
，求
的度数；
（2）如图2，创新小组的同学把直线
向上平移，并把的位置改变，发现
，说明理由；
实践探究：
（3）缜密小组在创新小组发现结论的基础上，将如图中的图形继续变化得到如图，
平分
，此时发现
与又存在新的数量关系，请直接写出与的数量关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知反比例函数 
的图象经过点A（1，3）．
（1）试确定此反比例函数的解析式；
（2）当x=2时，求y的值；
（3）当自变量x从5增大到8时，函数值y是怎样变化的？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小明准备测量一段水渠的深度，他把一根竹竿AB竖直插到水底，此时竹竿AB离岸边点C处的距离
米。竹竿高出水面的部分AD长0.5米，如果把竹竿的顶端A拉向岸边点C处，竿顶和岸边的水面刚好相齐，则水渠的深度BD为（ ）
A. 2米B. 2.5米C. 2.25米D. 3米
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，A、B、C三点的坐标分别为（﹣6，7）、（﹣3，0）、（0，3）．
（1）画出△ABC，并求△ABC的面积；
（2）在△ABC中，点C经过平移后的对应点为C′（5，4），将△ABC作同样的平移得到△A′B′C′， 画出平移后的△A′B′C′，并写出点A′，B′的坐标；
（3）已知点P（﹣3，m）为△ABC内一点，将点P向右平移4个单位后，再向下平移6个单位得到点Q（n，﹣3），则m= ，n= ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
