
【题目】在平面直角坐标系中,已知点A在y轴的正半轴上,点B在第二象限,AO=a,AB=b,BO与x轴正方向的夹角为150°,且a2b2+ab=0.
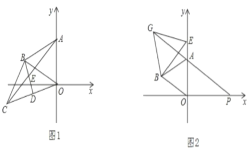
(1)试判定△ABO的形状;
(2)如图1,若BC⊥BO,BC=BO,点D为CO的中点,AC、BD交于E,求证:AE=BE+CE;
(3)如图2,若点E为y轴的正半轴上一动点,以BE为边作等边△BEG,延长GA交x轴于点P,问:AP与AO之间有何数量关系?试证明你的结论.
【答案】(1)△AOB为等边三角形,理由见解析;(2)见解析;(3)AP=2AO,证明见解析;
【解析】
(1)△ABO为等边三角形,理由为:根据(a2-b2)+(a-b)=0,得到a=b,再由BO与x轴正方向的夹角为150°得到∠AOB=60°,即可得证;
(2)在AC上截取AM=CE,先证∠AEB=60°,方法是根据题意得到△ABO为等边三角形,△BOC为等腰直角三角形,确定出∠ABD度数,根据AB=BC,且∠ABC=120°,得到∠BAE度数,进而确定出∠AEB为60°,再由AM=CE,得到AE=CM,再由AB=CB,且夹角∠BAC=∠BCA,利用SAS得到△BCM与△BAE全等,利用全等三角形的对应边相等得到BM=BE,得到△BEM为等边三角形,得到BE=EM,由AE=EM+AM,等量代换即可得证;
(3)AP=2AO,理由为:由题意得到BG=BE,AB=OB,利用等式的性质得到∠ABG=∠OBE,利用SAS得到△ABG与△OBE全等,利用全等三角形的对应角相等得到∠GAB=∠BOE=60°,利用外角的性质得到∠APO=30°,在Rt△AOP中,利用30度角所对的直角边等于斜边的一半得到AP=2AO.
(1)结论:△ABO为等边三角形,
理由:∵a2b2+ab=(a+b)(ab)+(ab)=(ab)(a+b+1)=0,
∴ab=0,得到a=b,即AO=AB
∵OB与x轴正半轴夹角为150°
∴∠AOB=150°90°=60°
∴△AOB为等边三角形;
(2)证明:在AC上截取AM=EC,可得AM+EM=CE+EM,即AE=CM.
∵△AOB为等边三角形,△BOC为等腰直角三角形
∴∠OBC=90°,∠ABO=60°
∵D为CO的中点
∴BD平分∠OBC,即∠CBD=∠OBD=45°
∴∠ABD=105°,∠ABC=150°
∴∠BAC=∠BCA=15°
∴∠AEB=60°
在△ABE和△CBM中
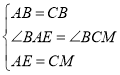 ,
,
∴△ABE≌△CBM(SAS)
∴BM=BE
∴△BEM为等边三角形
∴BE=EM
∴AE=AM+EM=CE+BE;
(3)结论:AP=2AO,
理由:∵△AOB与△BGE都为等边三角形
∴BE=BG,AB=OB,∠EBG=∠OBA=60°
∴∠EBG+∠EBA=∠OBA+∠EBA
即∠ABG=∠OBE
在△ABG和△OBE中
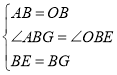 ,
,
∴△ABG≌△OBE(SAS)
∴∠BAG=∠BOE=60°
∴∠GAO=∠GAB+∠BAO=120°
∵∠GAO为△AOP的外角
且∠AOP=90°
∴∠APO=30°
在Rt△AOP中,∠APO=30°
∴AP=2AO.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )
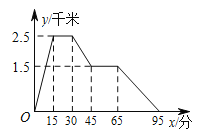
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)定义:直角三角形两直角边的平方和等于斜边的平方。如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=___.

(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP=![]() AD,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为多少?
AD,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A. B两种园艺造型共50个,摆放在迎宾大道两侧。已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆。
(1)某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )

A. 45°B. 60°C. 50°D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长.
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且速度都为1cm/s,连接AQ、CP交于点M,下面四个结论:①BP=CM;②△ABQ≌△CAP;③∠CMQ的度数不变,始终等于60°;④当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形,正确的有几个 ( )
秒时,△PBQ为直角三角形,正确的有几个 ( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com