
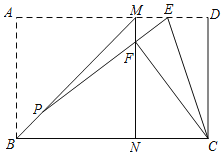
【题目】如图,在矩形纸片ABCD中,将AB沿BM翻折,使点A落在BC上的点N处,BM为折痕,连接MN;再将CD沿CE翻折,使点D恰好落在MN上的点F处,CE为折痕,连接EF并延长交BM于点P,若AD=8,AB=5,则线段PE的长等于_____.
【答案】![]()
【解析】
根据折叠可得ABNM是正方形,CD=CF=5,∠D=∠CFE=90![]() ,ED=EF,可求出三角形FNC的三边为3,4,5,在Rt△MEF中,由勾股定理可以求出三边的长,通过作辅助线,可证△FNC∽△PGF,三边占比为3:4:5,设未知数,通过PG=HN,列方程求出待定系数,进而求出PF的长,然后求PE的长.
,ED=EF,可求出三角形FNC的三边为3,4,5,在Rt△MEF中,由勾股定理可以求出三边的长,通过作辅助线,可证△FNC∽△PGF,三边占比为3:4:5,设未知数,通过PG=HN,列方程求出待定系数,进而求出PF的长,然后求PE的长.
过点P作PG⊥FN,PH⊥BN,垂足为G、H,
由折叠得:ABNM是正方形,AB=BN=NM=MA=5,
CD=CF=5,∠D=∠CFE=90![]() ,ED=EF,
,ED=EF,
∴NC=MD=8﹣5=3,
在Rt△FNC中,FN=![]() =4,
=4,
∴MF=5﹣4=1,
在Rt△MEF中,设EF=x,则ME=3﹣x,由勾股定理得,
12+(3﹣x)2=x2,
解得:x=![]() ,
,
∵∠CFN+∠PFG=90![]() ,∠PFG+∠FPG=90
,∠PFG+∠FPG=90![]() ,
,
∴∠CFN=∠PFG
∴△FNC∽△PGF,
∴FG:PG:PF=NC:FN:FC=3:4:5,
设FG=3m,则PG=4m,PF=5m,
∴GN=PH=BH=4﹣3m,HN=5﹣(4﹣3m)=1+3m=PG=4m,
解得:m=1,
∴PF=5m=5,
∴PE=PF+FE=5+![]() =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
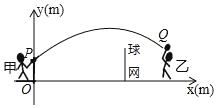
【题目】如图是甲、乙两人进行羽毛球练习赛时的一个瞬间,羽毛球飞行的高度y(m)与水平距离x(m)的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,已知点O与球网的水平距离为5m,球网的高度为1.55m.羽毛球沿水平方向运动4m时,达到羽毛球距离地面最大高度是![]() m.
m.
(1)求羽毛球经过的路线对应的函数关系式;
(2)通过计算判断此球能否过网;
(3)若甲发球过网后,羽毛球飞行到离地面的高度为![]() m的Q处时,乙扣球成功求此时乙与球网的水平距离.
m的Q处时,乙扣球成功求此时乙与球网的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过圆外一点P作⊙O的两条切线,切点分别为A、B,连接AB,在AB、PB、PA上分别取一点D、E、F,使AD=BE,BD=AF,连接DE、DF、EF,则∠EDF等于( )
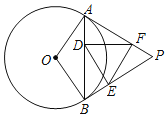
A.90°﹣∠PB.90°﹣![]() ∠PC.180°﹣∠PD.45°﹣
∠PC.180°﹣∠PD.45°﹣![]() ∠P
∠P
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OC是⊙O的半径,点D是半圆AB上一动点(不与A、B重合),连结DC交直径AB与点E,若∠AOC=60°,则∠AED的范围为( )
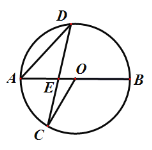
A.0°< ∠AED <180°B.30°< ∠AED <120°
C.60°< ∠AED <120°D.60°< ∠AED <150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A(0,﹣4)和B(2,0)两点.
(1)求c的值及a,b满足的关系式;
(2)若抛物线在A和B两点间,y随x的增大而增大,求a的取值范围;
(3)抛物线同时经过两个不同的点M(p,m),N(﹣2﹣p,n).
①若m=n,求a的值;
②若m=﹣2p﹣3,n=2p+1,点M在直线y=﹣2x﹣3上,请验证点N也在y=﹣2x﹣3上并求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() (x>0)交于点
(x>0)交于点![]() .
.

(1)求a,k的值;
(2)已知直线![]() 过点
过点![]() 且平行于直线
且平行于直线![]() ,点P(m,n)(m>3)是直线
,点P(m,n)(m>3)是直线![]() 上一动点,过点P分别作
上一动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线,交双曲线
轴的平行线,交双曲线![]() (x>0)于点
(x>0)于点![]() 、
、![]() ,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为
,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为![]() .横、纵坐标都是整数的点叫做整点.
.横、纵坐标都是整数的点叫做整点.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;②若区域
内的整点个数;②若区域![]() 内的整点个数不超过8个,结合图象,求m的取值范围.
内的整点个数不超过8个,结合图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,当自变量![]() 取
取![]() 时,函数值
时,函数值![]() 等于
等于![]() ,我们称
,我们称![]() 为这个函数的“二合点”.如果二次函数
为这个函数的“二合点”.如果二次函数![]() 有两个相异的二合点
有两个相异的二合点![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com