
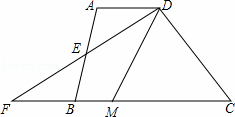
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点M在BC边上,且∠MDF=∠ADF.
(1)求证:△ADE≌△BFE.
(2)连接EM,如果FM=DM,判断EM与DF的关系,并说明理由.
科目:初中数学 来源: 题型:
下面调查统计中,适合做普查的是( ).
A.雪花牌电冰箱的市场占有率 B.蓓蕾专栏电视节目的收视率
C.飞马牌汽车每百公里的耗油量 D.今天班主任张老师与几名同学谈话
查看答案和解析>>
科目:初中数学 来源: 题型:
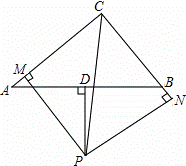
如图,在△ABC中,D是AB边的中点,PD⊥AB交∠ACB的平分线与点P,PM⊥AC于点M,PN⊥BC交CB的延长线于点N.
求证:CM=CN=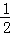 (AC+BC)
(AC+BC)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com