
【题目】(1)如图,直线L过A,B两点,请计算该直线的函数表达式。

(2)试判断:点P(1,-2)在不在直线L上?说说你的理由。
(3)求△AOB的面积
(4)当x取什么值时,y>0
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b(k≠0)的图象经过点A(2,-6),且与反比例函数y=-![]() 的图象交于点B(a,4)
的图象交于点B(a,4)
(1)求一次函数的解析式;
(2)将直线AB向上平移10个单位后得到直线l:y1=k1x+b1(k1≠0),l与反比例函数y2= ![]() 的图象相交,求使y1<y2成立的x的取值范围.
的图象相交,求使y1<y2成立的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
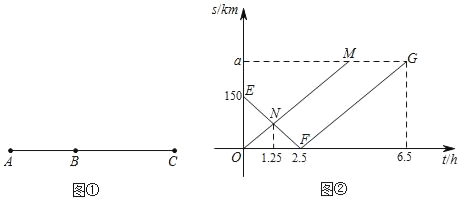
【题目】如图①,A、B、C三地依次在一直线上,两辆汽车甲、乙分别从A、B两地同时出发驶向C地,如图②,是两辆汽车行驶过程中到C地的距离s(km)与行驶时间t(h)的关系图象,其中折线段EF﹣FG是甲车的图象,线段OM是乙车的图象.
(1)图②中,a的值为 ;点M的坐标为 ;
(2)当甲车在乙车与B地的中点位置时,求行驶的时间t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种折叠式可调节的鱼竿支架的示意图,AE是地插,用来将支架固定在地面上,支架AB可绕A点前后转动,用来调节AB与地面的夹角,支架CD可绕AB上定点C前后转动,用来调节CD与AB的夹角,支架CD带有伸缩调节长度的伸缩功能,已知BC=60cm.
(1)若支架AB与地面的夹角∠BAF=35°,支架CD与钓鱼竿DB垂直,钓鱼竿DB与地面AF平行,则支架CD的长度为 cm(精确到0.1cm);(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70).
(2)如图2,保持(1)中支架AB与地面的夹角不变,调节支架CD与AB的夹角,使得∠DCB=85°,若要使钓鱼竿DB与地面AF仍然保持平行,则支架CD的长度应该调节为多少?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形与中间的小正方形拼成的一个大正方形如果大正方形的面积是13,小正方形的面积是4,直角三角形的较短直角边为a,较长直角边为b,那么![]() 的值为______________.
的值为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用配方法求出抛物线![]() 的顶点坐标、对称轴、最大值或最小值;若将抛物线
的顶点坐标、对称轴、最大值或最小值;若将抛物线![]() 先向左平移
先向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,所得抛物线的函数关系式为________.
个单位,所得抛物线的函数关系式为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与两坐标轴分别交于
的图象与两坐标轴分别交于![]() ,
,![]() ,
,![]() 三点,一次函数的图象与抛物线交于
三点,一次函数的图象与抛物线交于![]() ,
,![]() 两点.
两点.

![]() 求点
求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
![]() 当两函数的函数值都随着
当两函数的函数值都随着![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围;
的取值范围;
![]() 当自变量
当自变量![]() 满足什么范围时,一次函数值大于二次函数值.
满足什么范围时,一次函数值大于二次函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列各题:
(1)先化简,再求代数式(![]() 的值,其中x=
的值,其中x=![]() cos30°+
cos30°+![]() ;
;
(2)已知α是锐角,且sin(α+15°)=![]() .计算
.计算![]() -4cosα-(π-3.14)0+tanα+(
-4cosα-(π-3.14)0+tanα+(![]() )-1的值.
)-1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,A(0,3),B(4,0),C(﹣1,﹣1),点 P 线段 AB上一动点,将线段 AB 绕原点 O 旋转一周,点 P 的对应点为 P′,则 P′C 的最大值为_____,最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com