
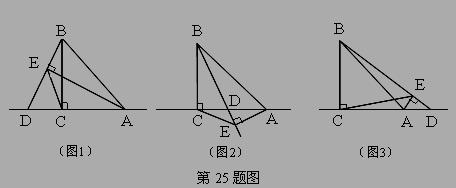
已知,在△ABC中,∠ACB=90°,CA=CB,D是直线AC上一点,连接BD,作AE⊥BD,垂足为E,连接EC.
(1)如图1,D在AC延长线上,AC > CD,求证:EA-EB=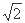 EC;
EC;
(2)当D在AC上(图2)或D在CA延长线上(图3)时,EA、EB、EC三条线段的数量关系如何?直接写出你探究的结论.
 |
(1)证明:在AE上截取AF=EB,连接CF--------1
∵AE⊥BD
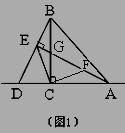 ∴∠AEB=90°
∴∠AEB=90°
∴∠AEB=∠ACB=90°
又∵∠AGC=∠BGE
∴∠GAC=∠GBE------------------------------------------------2
又∵CA=CB,AF=BE
∴△FAC≌△EBC---------------------------------------------------------------------------3
∴FC=EC,∠ ACF=∠BCE
∴∠ECF=∠BCE+∠GCF=∠ ACF+∠GCF=∠ACB=90°----------------------------4
∴EF=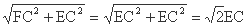 --------------------------------------5
--------------------------------------5
∴EA- EB= EA- AF= EF=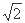 EC
EC
即EA- EB= 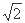 EC ---------------------------------------------------6
EC ---------------------------------------------------6
(2)当D在AC上(图2)时, EB- EA = 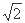 EC ---------
EC --------- ----------------9
----------------9
当 D在CA延长线上(图3)时,EA+EB= 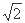 EC ----------------------12
EC ----------------------12


科目:初中数学 来源: 题型:
在“阳光体育”活动时间,甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中丙同学的概率;
(2)用画树状图或列表的方法,求恰好选中甲、乙两位同学进行比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,小明站在家中窗口选一个观测点D,测得正对面AB楼顶端A的仰角为30°,
楼底B的俯角为 15°,观测点D到楼AB的距离为27米.(结果用根号表示)
(1)求观测点D到楼顶A的距离;
(2)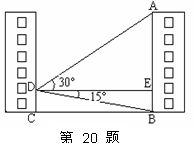 求楼AB的高度.
求楼AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
.某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票, 且行李费 y(元)是行李质量 x(千克)的一次函数,现已知李明带了 60 千克的行李费,交了行李 费 5 元;张华带了 90 千克的行李,交了行李费 10 元.
(1)写出 y 与 x 之间的函数表达式.
旅客最多可免费携带多少千克的行李?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是…………( )
A.28 B.29 C.30 D.31
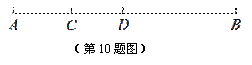 |
v
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com