Question

7．如图，在平面直角坐标系中，已知A（0，a）、B（-b，0）且a、b满足$\sqrt{a+b-4}$+|a-2b+2|=0．
（1）求证：∠OAB=∠OBA；
（2）如图1，若BE⊥AE，求∠AEO的度数；
（3）如图2，若D是AO的中点，DE∥BO，F在AB的延长线上，∠EOF=45°，连接EF，试探究OE和EF的数量和位置关系．

Answer 1

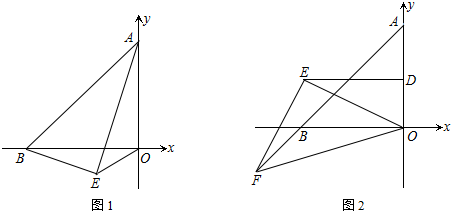
分析 （1）根据非负数的性质得到$\left\{\begin{array}{l}{a+b-4=0}\\{a-2b+2=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$，确定A（0，2）、B（-2，0），得到OA=OB，所以△AOB为等腰直角三角形，即可解答；
（2）如图1，过点O作OF⊥OE交AE于F，利用已知条件证明△OBE≌△OAF（ASA），得到OE=OF，即△OEF为等腰直角三角形，即可解答；
（3）过点F作FG⊥OF交OE的延长线于G，过点F作FH⊥FB交x轴于H，延长DE交HG于I，利用已知条件证明△HFG≌△BFO（SAS），得到FG=FO，GH=OB=OA，进而得到△FGO为等腰直角三角形，再证明△EIG≌△EDO（SAS）得到EG=EO，进而FE=EO且FE⊥EO（三线合一）．

解答 解：（1）∵a、b满足$\sqrt{a+b-4}$+|a-2b+2|=0．
∴$\left\{\begin{array}{l}{a+b-4=0}\\{a-2b+2=0}\end{array}\right.$
∴$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$，
∴A（0，2）、B（-2，0），
∴OA=OB，
∴△AOB为等腰直角三角形
∴∠OAB=∠OBA=45°，
（2）如图1，过点O作OF⊥OE交AE于F，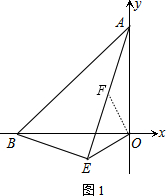

∵∠AOF+∠BOF=90°，∠BOE+∠BOF=90°
∴∠AOF=∠BOE，
∵BE⊥AE，
∴∠AEB=90°
又∠AOB=90°
∴∠OBE=∠AOF
在△OBE和△OAF中，$\left\{\begin{array}{l}∠OBE=∠OAF\\ OB=OA\\∠BOE=∠AOF\end{array}\right.$
∴△OBE≌△OAF（ASA）
∴OE=OF
∴△OEF为等腰直角三角形
∴∠AEO=45°
（3）过点F作FG⊥OF交OE的延长线于G，过点F作FH⊥FB交x轴于H，延长DE交HG于I，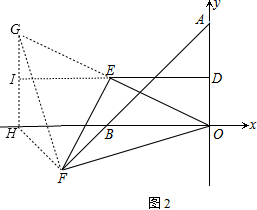

∵∠EOF=45°，∠HBF=∠ABO=45°，
∴△OFG、△HFB为等腰直角三角形，
∵∠HFG+∠GFB=90°，∠BFO+∠GFB=90°
∴∠HFG=∠BFO，
在△HFG和△BFO中，$\left\{\begin{array}{l}HF=FB\\∠HFG=∠BFO\\ FG=FO\end{array}\right.$
∴△HFG≌△BFO（SAS）
∴FG=FO，GH=OB=OA
∴△FGO为等腰直角三角形，
又∠GHF=∠OBF=135°
∴∠GHO=90°
∴HI=OD=IG
在△EIG和△EDO中，$\left\{\begin{array}{l}∠EIG=∠EDO\\∠IEG=∠DEO\\ IG=DO\end{array}\right.$
∴△EIG≌△EDO（SAS）
∴EG=EO
∴FE=EO且FE⊥EO（三线合一）．

点评 本题考查了非负数的性质、全等三角形的性质定理与判定定理，解决本题的关键是作出辅助线，构建全等三角形，利用全等三角形的对应边相等得到相等的线段．