
科目:初中数学 来源: 题型:
A、单项式-
| ||||
B、单项式-
| ||||
| C、多项式-6x2y-5xy2+8xy-7的次数是4 | ||||
| D、单项式a的次数是0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 一副风景画的长90cm,宽40cm(如图是其尺寸图),现要制作一个画框把它装入其中便于悬挂,制作的画框的四周的宽度一样,且要求风景画的面积是整个挂画面积的72%.
一副风景画的长90cm,宽40cm(如图是其尺寸图),现要制作一个画框把它装入其中便于悬挂,制作的画框的四周的宽度一样,且要求风景画的面积是整个挂画面积的72%.查看答案和解析>>
科目:初中数学 来源: 题型:
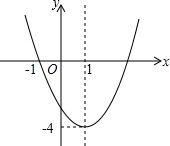 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )| A、二次函数的图象关于直线x=1对称 |
| B、当x>1时,y随x的增大而减小 |
| C、-1和3是方程ax2+bx+c=0(a≠0)的两个根 |
| D、函数y=ax2+bx+c(a≠0)的最小值是-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
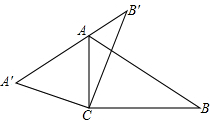 在图中,△ABC为直角三角形,∠ACB=90°,∠B=30°,以点C为旋转中心,将△ABC旋转到△A′B′C′的位置,使A′B′经过点A.
在图中,△ABC为直角三角形,∠ACB=90°,∠B=30°,以点C为旋转中心,将△ABC旋转到△A′B′C′的位置,使A′B′经过点A.查看答案和解析>>
科目:初中数学 来源: 题型:
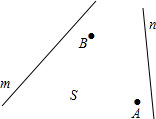 如图,某公司要在公路m,n之间的S区域修建一所物流中心P.按照设计要求,物流中心P到区域S内的两个社区A、B的距离必须相等,到两条公路m、n的距离也必须相等.那么物流中心P应建在什么位置才符合设计要求?请你在图中画出它的位置并标出所求.(保留画图痕迹)
如图,某公司要在公路m,n之间的S区域修建一所物流中心P.按照设计要求,物流中心P到区域S内的两个社区A、B的距离必须相等,到两条公路m、n的距离也必须相等.那么物流中心P应建在什么位置才符合设计要求?请你在图中画出它的位置并标出所求.(保留画图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:
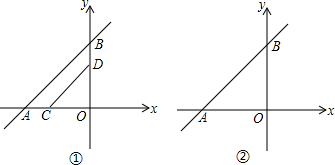
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com