
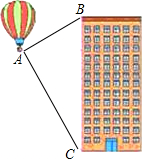
 如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为160$\sqrt{3}$米.
如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为160$\sqrt{3}$米. 分析 过A作AD⊥BC,垂足为D,在直角△ABD与直角△ACD中,根据三角函数的定义求得BD和CD,再根据BC=BD+CD即可求解.
解答 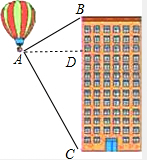 解:过A作AD⊥BC,垂足为D.
解:过A作AD⊥BC,垂足为D.
在Rt△ABD中,∵∠BAD=30°,AD=120m,
∴BD=AD•tan30°=120×$\frac{\sqrt{3}}{3}$=40$\sqrt{3}$m,
在Rt△ACD中,∵∠CAD=60°,AD=120m,
∴CD=AD•tan60°=120×$\sqrt{3}$=120$\sqrt{3}$m,
∴BC=BD+CD=40$\sqrt{3}$+120$\sqrt{3}$=160$\sqrt{3}$m.
故答案为:160$\sqrt{3}$.
点评 本题主要考查了解直角三角形的应用-仰角俯角问题,难度适中.对于一般三角形的计算,常用的方法是利用作高线转化为直角三角形的计算.


科目:初中数学 来源: 题型:选择题
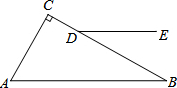 如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )
如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
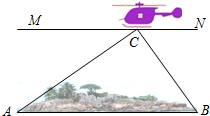 如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A、B的距离.
如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A、B的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com