
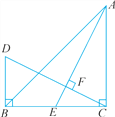
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作AE 的垂线CF,垂足为F,过点B作BD⊥BC,交CF的延长线于点D.
(1)求证:AE=CD.
(2)若AC=12 cm,求BD的长.
【答案】(1)证明见解析(2)6cm
【解析】(1)证两条线段相等,通常用全等,本题中的AE和CD分别在三角形AEC和三角形CDB中,在这两个三角形中,已经有一组边相等,一组角相等了,因此只需再找一组角即可利用角角边进行解答.
(2)由(1)得BD=EC=![]() BC=
BC=![]() AC,且AC=12,即可求出BD的长.
AC,且AC=12,即可求出BD的长.
(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,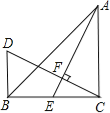
且BC=CA,
∴△DBC≌△ECA(AAS).
∴AE=CD.
(2)解:由(1)得AE=CD,AC=BC,
∴△CDB≌△AEC(HL),
∴BD=CE,
∵AE是BC边上的中线,
∴BD=EC=![]() BC=
BC=![]() AC,且AC=12cm.
AC,且AC=12cm.
∴BD=6cm.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
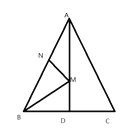
【题目】如图,在锐角△ABC中,AD平分∠BAC交BC于点D,点M,N分别是AD和AB上的动点,当SABC=6,AC=4时,BM+MN的最小值等于_______。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,是一个长为 2m,宽为 2n 的长方形,沿图中虚线用剪刀将其均分成四个完全相同的小长方形,然后按图 2 的形状拼图.
(1)图 2 中的图形阴影部分的边长为 ;(用含 m、n 的代数式表示)
(2)请你用两种不同的方法分别求图 2 中阴影部分的面积; 方法一: ;方法二: .
(3)观察图 2,请写出代数式(m+n)2、(m﹣n)2、4mn 之间的关系式: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
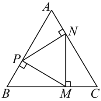
【题目】如图,点P,M,N分别在等边△ABC的各边上,且MP⊥AB,MN⊥BC,PN⊥AC.
(1)求证:△PMN是等边三角形;
(2)若AB=9 cm,求CM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.
(1)求证:△ACB∽△ADE;
(2)求AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:图1、图2是两张形状、大小完全相同的网格,网格中的每个小正方形的边长均为![]() .格中各有一个完全相同的三角形,请在图1、图2分别面一条直线,满足以下要求
.格中各有一个完全相同的三角形,请在图1、图2分别面一条直线,满足以下要求

(1)直线与三角形的交点要经过网格的格点(每个小正方形的顶点均为格点)
(2)在图1、图2中分别用不同的方法将三角形分成两个图形其中一个是三角形另一个是四边形,分割后的三角形的面积记为![]() ,四边形的面积为
,四边形的面积为![]() ,且
,且![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.
(1)求证:EF=DF﹣BE;
(2)若△ADF的周长为![]() ,求EF的长.
,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com