
【题目】如图:在等边三角形ABC中,点E在线段AB上,点D在CB的延长线上,![]()
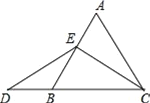
(1)试证明△DEC是等腰三角形;(2)在图中找出与AE相等的线段,并证明
【答案】(1)证明见解析;(2)BD=AE,证明见解析.
【解析】
(1)根据等边三角形的性质可得∠ABC=∠ACB,由三角形外角的性质可得∠ABC=∠D+∠DEB,再根据∠ACB=∠ACE+∠ECB,∠ACE=∠DEB,推得∠D=∠ECB即可得到结论;
(2)图中BD=AE,证明过程为:在AC上截取AF=AE,则可得△AEF是等边三角形,通过推导得出BE=CF,AE=EF,∠EFC=∠DBE,然后利用ASA证明△DEB≌△ECF,根据全等三角形的性质以及等量代换即可得.
(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵∠ABC是△DBE的外角,
∴∠ABC=∠D+∠DEB,
∵∠ACB=∠ACE+∠ECB,∠ACE=∠DEB,
∴∠D=∠ECB,
∴ED=EC,
即△DEC是等腰三角形;
(2)BD=AE,证明如下:
如图,在AC上截取AF=AE,
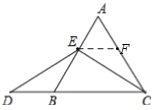
∵△ABC是等边三角形,
∴∠A=∠ABC=60°,AB=AC,
∴∠EBD=120°,AB-AE=AC-AF,△AEF是等边三角形,
∴BE=CF,AE=EF,∠AFE=60°,
∴∠EFC=120°,
∴∠EFC=∠DBE,
在△DBE和△EFC中,
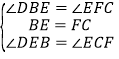 ,
,
∴△DEB≌△ECF,
∴BD=EF,
∴BD=AE.


科目:初中数学 来源: 题型:
【题目】(1) 知识储备
①如图 1,已知点 P 为等边△ABC 外接圆的弧BC 上任意一点.求证:PB+PC= PA.
②定义:在△ABC 所在平面上存在一点 P,使它到三角形三顶点的距离之和最小,则称点 P 为△ABC
的费马点,此时 PA+PB+PC 的值为△ABC 的费马距离.
(2)知识迁移
①我们有如下探寻△ABC (其中∠A,∠B,∠C 均小于 120°)的费马点和费马距离的方法:
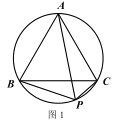
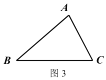
如图 2,在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆,根据(1)的结论,易知线段____的长度即为△ABC 的费马距离.
②在图 3 中,用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).
(3)知识应用
①判断题(正确的打√,错误的打×):
ⅰ.任意三角形的费马点有且只有一个(__________);
ⅱ.任意三角形的费马点一定在三角形的内部(__________).
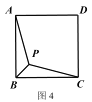
②已知正方形 ABCD,P 是正方形内部一点,且 PA+PB+PC 的最小值为![]() ,求正方形 ABCD 的
,求正方形 ABCD 的
边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连OB,将纸片OABC沿OB折叠,使点A落在A′的位置,若OB=![]() ,tan∠BOC=
,tan∠BOC=![]() ,则点A′的坐标( )
,则点A′的坐标( )

A. (![]() ,
,![]() ) B. (﹣
) B. (﹣![]() ,
,![]() ) C. (﹣
) C. (﹣![]() ,
,![]() ) D. (﹣
) D. (﹣![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,连结AC、BD,回答问题
(1)对角线AC、BD满足条件_____时,四边形EFGH是矩形.
(2)对角线AC、BD满足条件_____时,四边形EFGH是菱形.
(3)对角线AC、BD满足条件_____时,四边形EFGH是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:BM=CM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当矩形ABCD的长和宽满足什么条件时,四边形MENF是正方形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
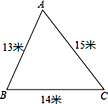
【题目】某小区内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化小区环境,预计花园每平方米造价为25元,小区修建这个花园需要投资多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com