
【题目】(1)课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.
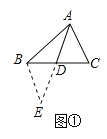
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
Ⅰ.由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
Ⅱ.由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
(2)如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长.

【答案】(1)Ⅰ.B;Ⅱ. 2<AD<11;(2)7
【解析】
(1)(Ⅰ)根据全等三角形的判定定理解答.
(Ⅱ)根据三角形的三边关系计算.
(2)延长AD到M,使AD=DM,连接BM,证明△ADC≌△MDB,根据全等三角形的性质解答.
解:(1)(Ⅰ)在△ADC和△EDB中,
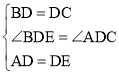 ,
,
∴△ADC≌△EDB(SAS),
故选:B;
(Ⅱ)∵△ADC≌△EDB,
∴BE=AC=9
∵AB﹣BE<AE<AB+BE,
∴4<AE<22
∴2<AD<11,
故答案为:2<AD<11.
(2)延长AD到M,使AD=DM,连接BM,如图②

∵AD是△ABC中线,
∴BD=DC,
∵在△ADC和△MDB中,
 ,
,
∴△ADC≌△MDB(SAS),
∴BM=AC,∠CAD=∠M,
∵∠AFE=∠AEF,
∴AE=EF=4,
∴AC=AE+CE=7,
∴BM=AC=7,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即AC=BF=7.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=(x﹣1)2﹣4,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠C=90°,∠A=34°,D,E 分别为 AB,AC 上一点,将△BCD,△ADE 沿 CD,DE 翻折,点 A,B 恰好重合于点 P 处,则∠ACP=_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若ΔPQR周长最小,则最小周长是()

A. 10 B. ![]() C. 20 D.
C. 20 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,花果山上有两只猴子在一棵树CD上的点B处,且BC=5m,它们都要到A处吃东西,其中一只猴子甲沿树爬下走到离树10m处的池塘A处,另一只猴子乙先爬到树顶D处后再沿缆绳DA线段滑到A处.已知两只猴子所经过的路程相等,设BD为xm.
(1)请用含有x的整式表示线段AD的长为______m;
(2)求这棵树高有多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A为某旅游景区的最佳观景点,游客可以在B处乘坐缆车沿BD方向先到达小观景平台DE观景,然后再由E处继续乘坐缆车沿EA方向到达A处,返程时从A处乘坐升降电梯直接到C处.已知AC⊥BC于C,DE∥BC,斜坡BD的坡度i=4:3,BC=210米,DE=48米,BD=100米,α=64°,则AC的高度为( )米(结果精确到0.1米,参考数据:sin64°≈0.9,tan64°≈2.1)

A. 214.2 B. 235.2 C. 294.2 D. 315.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。
(1)求∠EBC的度数;
(2)求证:BD=CD。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,BC=5.
⑴ 利用直尺和圆规在AB边上求作一点P,使得∠APC+∠BCP=90°,并说明理由;(不写作法,保留作图痕迹)
⑵ 在⑴的条件下,试判断∠PCB与∠A之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
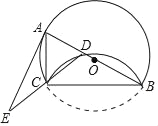
【题目】如图,以AB为直径作⊙O,点C为⊙O上一点,劣弧CB沿BC翻折,交AB于点D,过A作⊙O的切线交DC的延长线于点E.
(1)求证:AC=CD;
(2)已知tanE=![]() ,AC=2,求⊙O的半径.
,AC=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com