
【题目】情境观察: 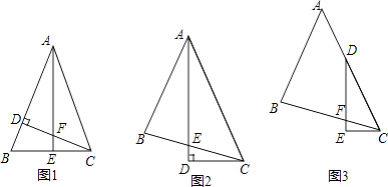
(1)如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F. ①写出图1中所有的全等三角形;
②线段AF与线段CE的数量关系是 .
(2)如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E. 求证:AE=2CD.
(3)如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC= ![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE. 要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE. 要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
【答案】
(1)△ABE≌△ACE,△ADF≌△CDB;AF=2CE 问题探究:
(2)证明:延长AB、CD交于点G,如图2‘所示:
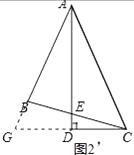
∵AD平分∠BAC,
∴∠CAD=∠GAD,
∵AD⊥CD,
∴∠ADC=∠ADG=90°,
在△ADC和△ADG中,
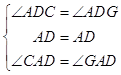 ,
,
∴△ADC≌△ADG(ASA),
∴CD=GD,即CG=2CD,
∵∠BAC=45°,AB=BC,
∴∠ABC=90°,
∴∠CBG=90°,
∴∠G+∠BCG=90°,
∵∠G+∠BAE=90°,
∴∠BAE=∠BCG,
在△ABE和△CBG中,
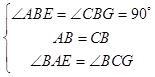 ,
,
∴△ADC≌△CBG中(ASA),
∴AE=CG=2CD
拓展延伸:
(3)解:作DG⊥BC交CE的延长线于G,
如图3所示.
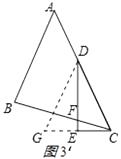
【解析】情境观察:解:①图1中所有的全等三角形为△ABE≌△ACE,△ADF≌△CDB;所以答案是:△ABE≌△ACE,△ADF≌△CDB②线段AF与线段CE的数量关系是:AF=2CE;所以答案是:AF=2CE. 情境观察:①由全等三角形的判定方法容易得出结果;②由全等三角形的性质即可得出结论;问题探究:延长AB、CD交于点G,由ASA证明△ADC≌△ADG,得出对应边相等CD=GD,即CG=2CD,证出∠BAE=∠BCG,由ASA证明△ADC≌△CBG,得出AE=CG=2CD即可.拓展延伸:作DG⊥BC交CE的延长线于G,同上证明三角形全等,得出DF=CG即可.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N
(1)求证:AE=MN;
(2)若AE=2,∠DAE=30°,求正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知1微米=10﹣7米,则25微米用科学记数法表示为( )
A.0.25×10﹣5米
B.25×10﹣7米
C.2.5×10﹣6米
D.2.5×10﹣8米
查看答案和解析>>
科目:初中数学 来源: 题型:
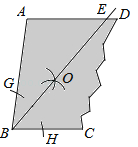
【题目】如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于![]() GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
(1)求证:AB=AE;
(2)若∠A=100°,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE、下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( ) 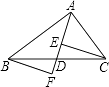
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A、C、B不在同一条直线上,AD∥BE
(1)如图①,当∠A=58°,∠B=118°时,求∠C的度数;
(2)如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;
(3)如图③,在(2)的前提下,且有AC∥QB,QP⊥PB,直接写出∠DAC:∠ACB:∠CBE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定满足( )
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对角线相等且相互平分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com