
【题目】已知:点A、C、B不在同一条直线上,AD∥BE
(1)如图①,当∠A=58°,∠B=118°时,求∠C的度数;
(2)如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;
(3)如图③,在(2)的前提下,且有AC∥QB,QP⊥PB,直接写出∠DAC:∠ACB:∠CBE的值.
【答案】
(1)解:在图①中,过点C作CF∥AD,则CF∥BE.

∵CF∥AD∥BE,
∴∠ACF=∠A,∠BCF=180°﹣∠B,
∴∠ACB=∠ACF+∠BCF=180°﹣(∠B﹣∠A)=120°.
(2)解:在图②中,过点Q作QM∥AD,则QM∥BE.
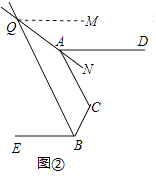
∵QM∥AD,QM∥BE,
∴∠AQM=∠NAD,∠BQM=∠EBQ.
∵AQ平分∠CAD,BQ平分∠CBE,
∴∠NAD= ![]() ∠CAD,∠EBQ=
∠CAD,∠EBQ= ![]() ∠CBE,
∠CBE,
∴∠AQB=∠BQM﹣∠AQM= ![]() (∠CBE﹣∠CAD).
(∠CBE﹣∠CAD).
∵∠C=180°﹣(∠CBE﹣∠CAD)=180°﹣2∠AQB,
∴2∠AQB+∠C=180°.
(3)解:∵AC∥QB,
∴∠AQB=∠CAP= ![]() ∠CAD,∠ACP=∠PBQ=
∠CAD,∠ACP=∠PBQ= ![]() ∠CBE,
∠CBE,
∴∠ACB=180°﹣∠ACP=180°﹣ ![]() ∠CBE.
∠CBE.
∵2∠AQB+∠ACB=180°,
∴∠CAD= ![]() ∠CBE.
∠CBE.
又∵QP⊥PB,
∴∠CAP+∠ACP=90°,即∠CAD+∠CBE=180°,
∴∠CAD=60°,∠CBE=120°,
∴∠ACB=180°﹣(∠CBE﹣∠CAD)=120°,
∴∠DAC:∠ACB:∠CBE=60°:120°:120°=1:2:2.
【解析】(1)过点C作CF∥AD,依据平行公理的推论可知CF∥BE,接下来,根据平行线的性质可得出∠ACF=∠A、∠BCF=180°-∠B,将其代入∠ACB=∠ACF+∠BCF即可求出∠ACB的度数;
(2)过点Q作QM∥AD,依据平行公理的推论可知QM∥BE,接下来,根据平行线的性质、角平分线的定义可得出∠AQB=![]() (∠CBE-∠CAD),结合(1)的结论可得出2∠AQB+∠C=180°;
(∠CBE-∠CAD),结合(1)的结论可得出2∠AQB+∠C=180°;
(3)由(2)的结论可得出∠CAD=![]() ∠CBE①,由QP⊥PB可得出∠CAD+∠CBE=180°②,联立①②可求出∠CAD、∠CBE的度数,再结合(1)的结论可得出∠ACB的度数,将其代入∠DAC:∠ACB:∠CBE中可求出结论.
∠CBE①,由QP⊥PB可得出∠CAD+∠CBE=180°②,联立①②可求出∠CAD、∠CBE的度数,再结合(1)的结论可得出∠ACB的度数,将其代入∠DAC:∠ACB:∠CBE中可求出结论.
【考点精析】根据题目的已知条件,利用平行线的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】情境观察: 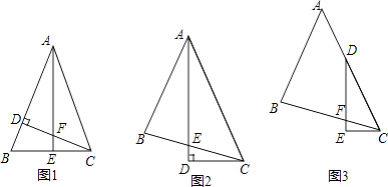
(1)如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F. ①写出图1中所有的全等三角形;
②线段AF与线段CE的数量关系是 .
(2)如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E. 求证:AE=2CD.
(3)如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC= ![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE. 要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE. 要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接MN,DN.请你判定四边形BMDN是什么特殊四边形,并说明理由. 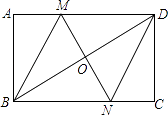
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.
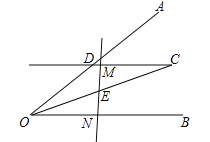
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( ) 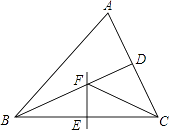
A.48°
B.36°
C.30°
D.24°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com