
【题目】问题背景:已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,记△ADM的面积为S1 , △BND的面积为S2 . 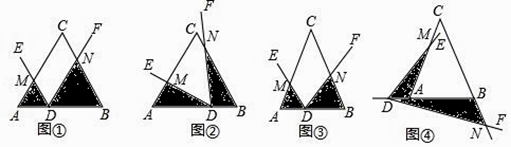
(1)初步尝试:如图①,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,则S1S2=;
(2)类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图②所示位置,求S1S2的值;
(3)延伸拓展:当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α.
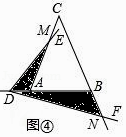
(Ⅰ)如图③,当点D在线段AB上运动时,设AD=a,BD=b,求S1S2的表达式(结果用a,b和α的三角函数表示).
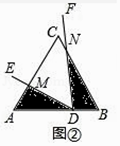
(Ⅱ)如图④,当点D在BA的延长线上运动时,设AD=a,BD=b,直接写出S1S2的表达式,不必写出解答过程.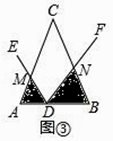
【答案】
(1)12
(2)
解:如图2中,设AM=x,BN=y.
∵∠MDB=∠MDN+∠NDB=∠A+∠AMD,∠MDN=∠A,
∴∠AMD=∠NDB,∵∠A=∠B,
∴△AMD∽△BDN,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴xy=8,
∵S1= ![]() ADAMsin60°=
ADAMsin60°= ![]() x,S2=
x,S2= ![]() DBsin60°=
DBsin60°= ![]() y,
y,
∴S1S2= ![]() x
x ![]() y=
y= ![]() xy=12
xy=12
(3)
解:Ⅰ如图3中,设AM=x,BN=y,
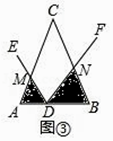
同法可证△AMD∽△BDN,可得xy=ab,
∵S1= ![]() ADAMsinα=
ADAMsinα= ![]() axsinα,S2=
axsinα,S2= ![]() DBBNsinα=
DBBNsinα= ![]() bysinα,
bysinα,
∴S1S2= ![]() (ab)2sin2α.
(ab)2sin2α.
Ⅱ如图4中,设AM=x,BN=y,
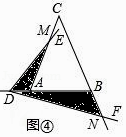
同法可证△AMD∽△BDN,可得xy=ab,
∵S1= ![]() ADAMsinα=
ADAMsinα= ![]() axsinα,S2=
axsinα,S2= ![]() DBBNsinα=
DBBNsinα= ![]() bysinα,
bysinα,
∴S1S2= ![]() (ab)2sin2α.
(ab)2sin2α.
【解析】解:(1)如图1中,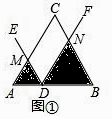
∵△ABC是等边三角形,
∴AB=CB=AC=6,∠A=∠B=60°,
∵DE∥BC,∠EDF=60°,
∴∠BND=∠EDF=60°,
∴∠BDN=∠ADM=60°,
∴△ADM,△BDN都是等边三角形,
∴S1= ![]() 22=
22= ![]() ,S2=
,S2= ![]() (4)2=4
(4)2=4 ![]() ,
,
∴S1S2=12,
所以答案是12.
【考点精析】本题主要考查了等腰三角形的性质和等边三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】设A= ![]() ÷(a﹣
÷(a﹣ ![]() ).
).
(1)化简A;
(2)当a=3时,记此时A的值为f(3);当a=4时,记此时A的值为f(4);… 解关于x的不等式: ![]() ﹣
﹣ ![]() ≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.
≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,小明从家到学校行驶路程s(m)与时间t(min)的大致图象是( )
A.
B.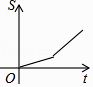
C.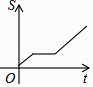
D.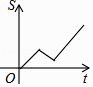
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与反比例函数y= ![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.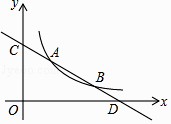
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF. 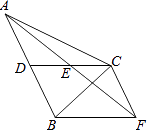
(1)求证:CF=AD;
(2)若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若记y=f(x)= ![]() ,其中f(1)表示当x=1时y的值, 即f(1)=
,其中f(1)表示当x=1时y的值, 即f(1)= ![]() =
= ![]() ;f(
;f( ![]() )表示当x=
)表示当x= ![]() 时y的值,即f(
时y的值,即f( ![]() )=
)= ![]()
![]() ;…;则f(1)+f(2)+f(
;…;则f(1)+f(2)+f( ![]() )+f(3)+f(
)+f(3)+f( ![]() )+…+f(2011)+f(
)+…+f(2011)+f( ![]() )= .
)= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题
(1)问题发现:
如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC,请判断:FG与CE的数量关系是 , 位置关系是 . 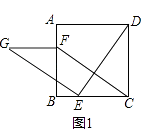
(2)拓展探究:
如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断予以证明;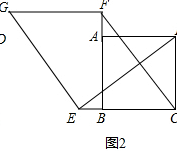
(3)类比延伸:
如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.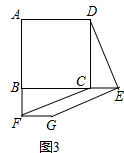
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com