
| 2 |
| 3 |
| 4 |
| 9 |
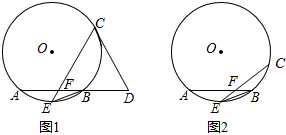
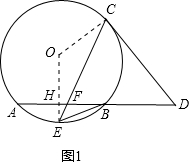
 |
| AE |
 |
| BE |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 7 |
| 9 |
| 7 |
| 9 |
| 2 |
| 9 |
| OA2-OH2 |
r2-(
|
4
| ||
| 9 |
| 1 |
| 2 |
2
| ||
| 9 |
| HE2+HF2 |
(
|
2
| ||
| 9 |
| 4 |
| 9 |
2
| ||
| 3 |


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
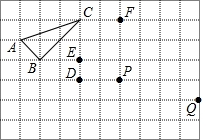 如图,在正方形格纸中,△ABC的三个顶点及D、E、F、P、Q五个点分别位于边长为1的小正方形的顶点上,先从P、Q两个点中任意取一个点,再从D、E、F三个点中任意取两个点,以所取的这三个点为顶点组成三角形,求所组成的三角形与△ABC相似的概率(用画树状图或列表法求解).
如图,在正方形格纸中,△ABC的三个顶点及D、E、F、P、Q五个点分别位于边长为1的小正方形的顶点上,先从P、Q两个点中任意取一个点,再从D、E、F三个点中任意取两个点,以所取的这三个点为顶点组成三角形,求所组成的三角形与△ABC相似的概率(用画树状图或列表法求解).查看答案和解析>>
科目:初中数学 来源: 题型:
| A、102×103 |
| B、10.2×104 |
| C、1.02×105 |
| D、0.102×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:
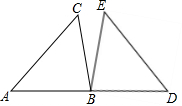 在△ABC中,∠A=45°,∠B=75°,BC=2,将Rt△ABC绕点B旋转至△BDE的位置,如图所示,且使A、B、D在同一条直线上,请在图中表示出AC边扫过的图形,并计算其面积.
在△ABC中,∠A=45°,∠B=75°,BC=2,将Rt△ABC绕点B旋转至△BDE的位置,如图所示,且使A、B、D在同一条直线上,请在图中表示出AC边扫过的图形,并计算其面积.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | ||
|
| 2 |
| 1 | ||||
|
| 3 |
| 2 |
| 1 | ||||
|
| 4 |
| 3 |
| 1 | ||||
|
| 1 | ||
1+
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com