
【题目】如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=4 ![]() ,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F
,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F 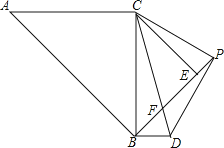
(1)求证: ![]() ;
;
(2)连接BD,请你判断AC与BD有什么位置关系?并说明理由;
(3)设PE=x,△PBD的面积为S,求S与x之间的函数关系式.
【答案】
(1)
证明:∵△BCE和△CDP均为等腰直角三角形,
∴∠ECB=∠PCD=45°,∠CEB=∠CPD=90°,
∴△BCE∽△DCP,
∴ ![]()
(2)
解:AC∥BD,
理由:∵∠PCE+∠ECD=∠BCD+∠ECD=45°,
∴∠PCE=∠BCD,
又∵ ![]() ,
,
∴△PCE∽△DCB,
∴∠CBD=∠CEP=90°,
∵∠ACB=90°,
∴∠ACB=∠CBD,
∴AC∥BD;
(3)
解:如图所示: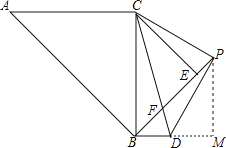
作PM⊥BD于M,
∵AC=4 ![]() ,△ABC和△BEC均为等腰直角三角形,
,△ABC和△BEC均为等腰直角三角形,
∴BE=CE=4,
∵△PCE∽△DCB,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴BD= ![]() x,
x,
∵∠PBM=∠CBD﹣∠CBP=45°,BP=BE+PE=4+x,
∴PM= ![]() ,
,
∴△PBD的面积S= ![]() BDPM=
BDPM= ![]() ×
× ![]() x×
x× ![]() =
= ![]() x2+2x.
x2+2x.
【解析】(1)直接利用相似三角形的判定方法得出△BCE∽△DCP,进而得出答案;
(2)首先得出△PCE∽△DCB,进而求出∠ACB=∠CBD,即可得出AC与BD的位置关系;
(3)首先利用相似三角形的性质表示出BD,PM的长,进而表示出△PBD的面积.此题主要考查了相似形综合、平行线的判定方法以及相似三角形的判定与性质等知识,正确表示出PM的长是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA=60°,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s),则点Q的运动速度为 cm/s,使得A、C、P三点构成的三角形与B、P、Q三点构成的三角形全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读)如图1,四边形OABC中,OA=a,OC=3,BC=2,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ [θ,a ]
(理解)若点D与点A重合,则这个操作过程为FZ [45°,3];
(尝试)
(1)若点D恰为AB的中点(如图2),求θ;
(2)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上(如图3),求出a的值;若点E落在四边形OABC的外部,直接写出a的取值范围.
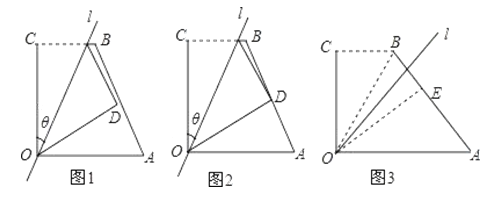
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是双曲线 ![]() 在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线
在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线 ![]() 上运动,则k的值是
上运动,则k的值是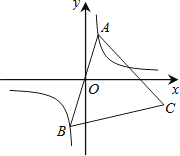
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级三班学生苏琪为帮助同桌万宇巩固“平面直角坐标系四个象限内及坐标轴上的点的坐标特点”这一基础知识,在三张完全相同且不透明的卡片正面分别写上了﹣3,0,2三个数字,背面向上洗匀后随机抽取一张,将卡片上的数字记为a,再从剩下的两张中随机取出一张,将卡片上的数字记为b,然后叫万宇在平面直角坐标系中找出点M(a,b)的位置.
(1)请你用树状图帮万宇同学进行分析,并写出点M所有可能的坐标;
(2)求点M在第二象限的概率;
(3)张老师在万宇同学所画的平面直角坐标系中,画了一个半径为3的⊙O,过点M能作多少条⊙O的切线?请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】表为甲班55人某次数学小考成绩的统计结果,关于甲班男、女生此次小考成绩的统计量,下列叙述何者正确?( )
成绩(分) | 50 | 70 | 90 |
男生(人) | 10 | 10 | 10 |
女生(人) | 5 | 15 | 5 |
合计(人) | 15 | 25 | 15 |
A.男生成绩的四分位距大于女生成绩的四分位距
B.男生成绩的四分位距小于女生成绩的四分位距
C.男生成绩的平均数大于女生成绩的平均数
D.男生成绩的平均数小于女生成绩的平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示,直线l过点M(3,0)且平行于y轴.
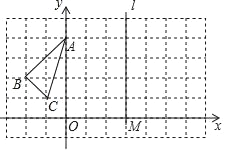
(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标.
(2)如果点P的坐标是(﹣a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求P1P2的长.(用含a的代数式表示)
(3)通过计算加以判断,PP2的长会不会随点P位置的变化而变化.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图![]() 所示放置,图
所示放置,图![]() 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
![]() 请找出图
请找出图![]() 中的全等三角形,并给予说明
中的全等三角形,并给予说明![]() 说明:结论中不得含有未标识的字母
说明:结论中不得含有未标识的字母![]() ;
;
![]() 试说明:
试说明:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com