
【题目】某校为了丰富学生课余生活,计划开设以下社团:A.足球、B.机器人、C.航模、D.绘画,学校要求每人只能参加一个社团小丽和小亮准备随机报名一个项目.
(1)求小亮选择“机器人”社团的概率为______;
(2)请用树状图或列表法求两人至少有一人参加“航模”社团的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;
;
【解析】
(1)属于求简单事件的概率,根据概率公式计算可得;
(2)用列表格法列出所有的等可能结果,从中确定符合事件的结果,根据概率公式计算可得.
解:(1)小亮随机报名一个项目共有4种等可能结果,分别为A.足球、B.机器人、C.航模、D.绘画,其中选择“机器人”的有1种,为B.机器人,所以选择“机器人”的概率为P=![]() .
.
(2)用列表法表示所有可能出现的结果如图:
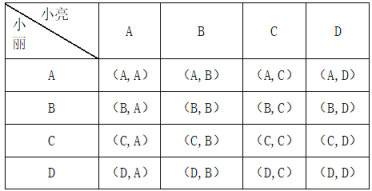
从表格可以看出,总共有16种结果,每种结果出现的可能性相同,其中至少有一人参加“航模”社团有7种,分别为(A,C),(B,C),(C,A), (C,B),(C,C), (C,D),(D,C),所以两人至少有一人参加“航模”社团的概率P=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
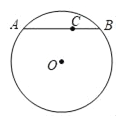
【题目】如图,AB为⊙O的弦,C为弦AB上一点,设AC=m,BC=n(m>n),将弦AB绕圆心O旋转一周,若线段BC扫过的面积为(m2﹣n2)π,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数y=-![]() 和y=
和y=![]() 的图象交于A点和B点.若C为x轴上任意一点,连接AC、BC,则△ABC的面积为 .
的图象交于A点和B点.若C为x轴上任意一点,连接AC、BC,则△ABC的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
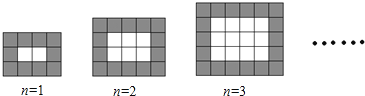
【题目】如图,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究在第n个图中,黑、白瓷砖分别各有多少块( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 、
、![]() 为常数)的图像经过点
为常数)的图像经过点![]() 和点
和点![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
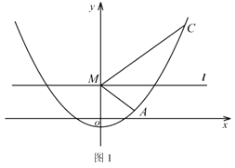
(2)如图1,点![]() 在抛物线上,点
在抛物线上,点![]() 是
是![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 平分
平分![]() ,求点
,求点![]() 的坐标;
的坐标;
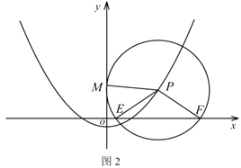
(3)如图2,在(2)的条件下,点![]() 是抛物线上的一动点,以
是抛物线上的一动点,以![]() 为圆心、
为圆心、![]() 为半径的圆与
为半径的圆与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
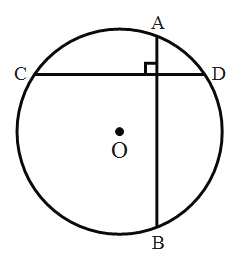
【题目】我们定义:如果圆的两条弦互相垂直,那么这两条弦互为“十字弦”,也把其中的一条弦叫做另一条弦的“十字弦”.如:如图,已知![]() 的两条弦
的两条弦![]() ,则
,则![]() 、
、![]() 互为“十字弦”,
互为“十字弦”,![]() 是
是![]() 的“十字弦”,
的“十字弦”,![]() 也是
也是![]() 的“十字弦”.
的“十字弦”.
(1)若![]() 的半径为5,一条弦
的半径为5,一条弦![]() ,则弦
,则弦![]() 的“十字弦”
的“十字弦”![]() 的最大值为______,最小值为______.
的最大值为______,最小值为______.
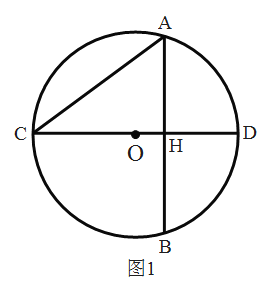
(2)如图1,若![]() 的弦
的弦![]() 恰好是
恰好是![]() 的直径,弦
的直径,弦![]() 与
与![]() 相交于
相交于![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() 、
、![]() 互为“十字弦”;
互为“十字弦”;
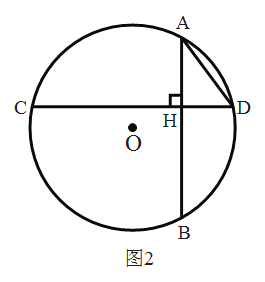
(3)如图2,若![]() 的半径为5,一条弦
的半径为5,一条弦![]() ,弦
,弦![]() 是
是![]() 的“十字弦”,连接
的“十字弦”,连接![]() ,若
,若![]() ,求弦
,求弦![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.
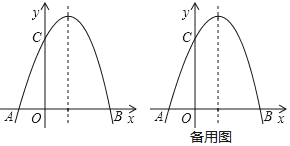
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=40°,点D、点E分别从点B、点C同时出发,在线段BC上作等速运动,到达C点、B点后运动停止.
(1)求证:△ABE≌△ACD;
(2)若AB=BE,求∠DAE的度数;
拓展:若△ABD的外心在其内部时,求∠BDA的取值范围.
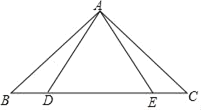
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华人民共和国《城市道路路内停车泊位设置规范》规定:
一、在城市道路范围内,在不影响行人、车辆通行的情况下,政府有关部门可以规划停车泊位.停车泊位的排列方式有三种,如图所示:
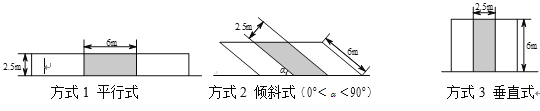
二、双向通行道路,路幅宽![]() 米以上的,可在两侧设停车泊位,路幅宽
米以上的,可在两侧设停车泊位,路幅宽![]() 米到
米到![]() 米的,可在单侧设停车泊位,路幅宽
米的,可在单侧设停车泊位,路幅宽![]() 米以下的,不能设停车泊位;
米以下的,不能设停车泊位;
三、规定小型停车泊位,车位长![]() 米,车位宽
米,车位宽![]() 米;
米;
四、设置城市道路路内机动车停车泊位后,用于单向通行的道路宽度应不小于![]() 米.
米.
根据上述的规定,在不考虑车位间隔线和车道间隔线的宽度的情况下,如果在一条路幅宽为![]() 米的双向通行车道设置同一种排列方式的小型停车泊位,请回答下列问题:
米的双向通行车道设置同一种排列方式的小型停车泊位,请回答下列问题:
(1)可在该道路两侧设置停车泊位的排列方式为 ;
(2)如果这段道路长![]() 米,那么在道路两侧最多可以设置停车泊位 个.
米,那么在道路两侧最多可以设置停车泊位 个.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com