
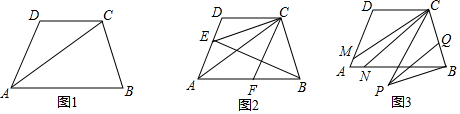
���� ��1�������ڴ�����ȣ���ֱ��ƽ�н���֤�����ɣ�
��2�����DCE=��ACE=�������CAB=2�������ݡ�ACB=��ABC���ɵá�ACB=90��-���������õ���BCE=90�㣬������CFƽ�֡�ECB���ɵá�ECF=$\frac{1}{2}$��BCE=45�㣻
��3�����������ε�һ����ǵ������������ڵ������ڽǵĺͣ��ɵá�1=��BPC+��ABP���ٸ���ƽ���ߵ������Լ���ƽ���ߵĶ����ʾ����MCP����DPQ��������ֱ��ƽ�У��ڴ�����ȿɵá�NCP=��CPQ��Ȼ����ʽ��ʾ����MCN=$\frac{1}{2}$��ABP���Ӷ��ж�����ȷ��
��� 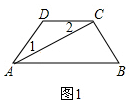 �⣺��1��AB��CD��
�⣺��1��AB��CD��
֤������ACƽ�֡�DAB��
���1=��CAB��
�ߡ�1=��2��
���2=��CAB��
��AB��CD��
��2����CEƽ�֡�DCA��AB��CD��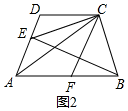
������DCE=��ACE=�������CAB=2����
�ߡ�ACB=��ABC��
���ABC����ACB=$\frac{1}{2}$��180��-��CAB��=90��-����
���BCE=��BCA+��ECA=90��-��+��=90�㣬
��CFƽ�֡�ECB��
���ECF=$\frac{1}{2}$��BCE=45�㣻
��3�����ۢ���ȷ��
��ͼ�����������ε�������ʿɵã���1=��BPC+��ABP�� ��PQƽ�֡�BPC��CMƽ�֡�DCP��
��PQƽ�֡�BPC��CMƽ�֡�DCP��
���CPQ=$\frac{1}{2}$��BPC����MCP=$\frac{1}{2}$��DCP��
��AB��CD��
���1=��DCP��
���MCP=$\frac{1}{2}$����BPC+��ABP����
��PQ��CN��
���NCP=��CPQ=$\frac{1}{2}$��BPC��
���MCN=��MCP-��NCP=$\frac{1}{2}$����BPC+��B��-$\frac{1}{2}$��BPC=$\frac{1}{2}$��ABP=$\frac{1}{2}$��30��=15�㣬
����ۢڡ�MCN�Ķ������䣬Ϊ15�㣮
���� ������Ҫ������ƽ���ߵ����ʣ���������������Լ��������ڽǺͶ������ۺ�Ӧ�ã�����ʱע�⣺�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ��������ڽǺ���180�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
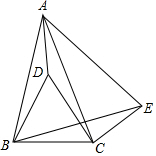 ��ͼ���ڡ�ABC�У�AB=AC����D�ڡ�ABC�ڣ�BD=BC����DBC=60�㣬��E�ڡ�ABC�⣬��BCE=150�㣬��ABE=60�㣮
��ͼ���ڡ�ABC�У�AB=AC����D�ڡ�ABC�ڣ�BD=BC����DBC=60�㣬��E�ڡ�ABC�⣬��BCE=150�㣬��ABE=60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
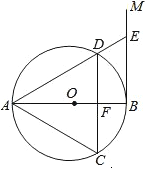 ��ͼ��AB�ǡ�O��ֱ��������B��BM��AB����CD��BM����AB�ڵ�F����DA=DC������AC��AD���ӳ�AD��BM�ڵ�E��
��ͼ��AB�ǡ�O��ֱ��������B��BM��AB����CD��BM����AB�ڵ�F����DA=DC������AC��AD���ӳ�AD��BM�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
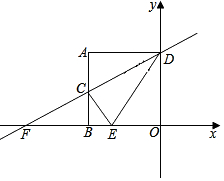 ��ͼ��������ABOD�ı߳�Ϊ2��OB��x���ϣ�OD��y���ϣ���AD��OB��AB��OD����CΪAB���е㣬ֱ��CD��x���ڵ�F��
��ͼ��������ABOD�ı߳�Ϊ2��OB��x���ϣ�OD��y���ϣ���AD��OB��AB��OD����CΪAB���е㣬ֱ��CD��x���ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
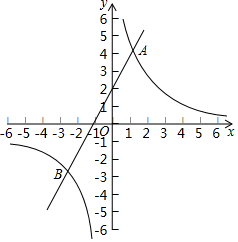 ��ͼ��ֱ��y=2x+n��˫����y=$\frac{m}{x}$��m��0������A��B���㣬�ҵ�A������Ϊ��1��4����
��ͼ��ֱ��y=2x+n��˫����y=$\frac{m}{x}$��m��0������A��B���㣬�ҵ�A������Ϊ��1��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
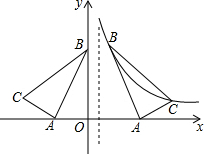 ��ͼ����ƽ��ֱ������ϵ����Rt��ABC����CAB=90�㣬A��-2��0����B��0��4������C�ڵڶ�������tan��ACB=2����Rt��ABC��ƽ����y���ij��ֱ�߷��ۣ���Rt��A1B1C1������B1��C1ǡ�����ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ���k��ֵ����$\frac{16}{3}$��
��ͼ����ƽ��ֱ������ϵ����Rt��ABC����CAB=90�㣬A��-2��0����B��0��4������C�ڵڶ�������tan��ACB=2����Rt��ABC��ƽ����y���ij��ֱ�߷��ۣ���Rt��A1B1C1������B1��C1ǡ�����ڷ���������y=$\frac{k}{x}$��x��0����ͼ���ϣ���k��ֵ����$\frac{16}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 5$\sqrt{2}$ | C�� | 5$\sqrt{3}$ | D�� | 3$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com