
分析 (1)y=(空调售价-空调进价)x+(彩电售价-彩电进价)×(30-x);
(2)根据用于一次性购进空调、彩电共30台,总资金为12.8万元,全部销售后利润不少于1.5万元.得到一元一次不等式组,求出满足题意的x的正整数值即可;
(3)利用y与x的函数关系式y=300x+12000的增减性来选择哪种方案获利最大,并求此时的最大利润即可.
解答 解:(1)设商场计划购进空调x台,则计划购进彩电(30-x)台,由题意,得
y=(6100-5400)x+(3900-3500)(30-x)=300x+12000(0≤x≤30);
(2)依题意,有$\left\{\begin{array}{l}{5400x+3500(30-x)≤128000\\;}\\{300x+12000≥15000}\end{array}\right.$,
解得10≤x≤12$\frac{2}{19}$.
∵x为整数,
∴x=10,11,12.
即商场有三种方案可供选择:
方案1:购空调10台,购彩电20台;
方案2:购空调11台,购彩电19台;
方案3:购空调12台,购彩电18台;
(3)∵y=300x+12000,k=300>0,
∴y随x的增大而增大,
即当x=12时,y有最大值,
y最大=300×12+12000=15600元.
故选择方案3:购空调12台,购彩电18台时,商场获利最大,最大利润是15600元.
点评 本题主要考查了一次函数和一元一次不等式组的实际应用,难度适中,得出商场获得的利润y与购进空调x的函数关系式是解题的关键.在解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
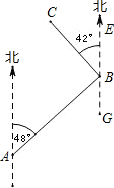 如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A、B两地同时开工,若干天后公路准确接通.若公路AB长10千米另一条公路BC长7千米,且BC的走向是北偏西42°,则A到公路BC的距离为( )
如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A、B两地同时开工,若干天后公路准确接通.若公路AB长10千米另一条公路BC长7千米,且BC的走向是北偏西42°,则A到公路BC的距离为( )| A. | 3 | B. | 7 | C. | 10 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
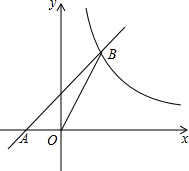 如图,直线y=kx+2k (k≠0)与x轴交于点A,与反比例函数y=(m+3)x2m-1在第一象限内的图象交于点B,已知S△AOB=3.
如图,直线y=kx+2k (k≠0)与x轴交于点A,与反比例函数y=(m+3)x2m-1在第一象限内的图象交于点B,已知S△AOB=3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
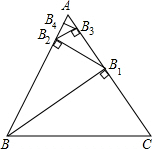 如图,△ABC是一个边长为1的等边三角形,BB1是△ABC的高,B1B2是△ABB1的高,B2B3是△AB1B2的高,…,Bn-1Bn是△ABn-2Bn-1的高,则Bn-1Bn的长是$\frac{\sqrt{3}}{{2}^{n}}$.
如图,△ABC是一个边长为1的等边三角形,BB1是△ABC的高,B1B2是△ABB1的高,B2B3是△AB1B2的高,…,Bn-1Bn是△ABn-2Bn-1的高,则Bn-1Bn的长是$\frac{\sqrt{3}}{{2}^{n}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
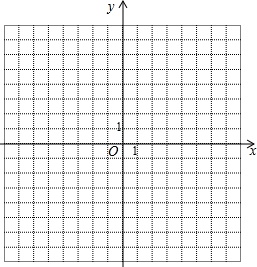 在如图所示的平面直角坐标系中完成下列任务:
在如图所示的平面直角坐标系中完成下列任务:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
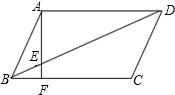 如图,在?ABCD中,∠ABC=72°,AF⊥BC于F,AF交BD于点E,若DE=2AB,则∠AED的大小是( )
如图,在?ABCD中,∠ABC=72°,AF⊥BC于F,AF交BD于点E,若DE=2AB,则∠AED的大小是( )| A. | 60° | B. | 66° | C. | 70° | D. | 72° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com