
【题目】解下列方程:
(1)![]() ;
;
(2)![]() ;
;
(3)(x+1)(x+2)(x+3)(x+4)=120;
【答案】(1)x1= 1,x2=![]() ,x3=
,x3=![]() .(2)x1=8,x2=﹣1,x3=﹣8,x4=1.(3)x1=﹣6,x2=1.
.(2)x1=8,x2=﹣1,x3=﹣8,x4=1.(3)x1=﹣6,x2=1.
【解析】
(1)把原方程变形为![]() +1+
+1+![]() =
=![]() ,设y=
,设y=![]() ,可得分式方程,解分式方程后解两个一元二次方程即可得答案;(2)设x2+2x﹣8=y,把原方程变形为
,可得分式方程,解分式方程后解两个一元二次方程即可得答案;(2)设x2+2x﹣8=y,把原方程变形为![]() +
+![]() +
+![]() =0,去分母后可得y=9x或y=﹣5x,代入x2+2x﹣8=y,解两个一元二次方程即可得答案;(3)根据题意可得[(x+1)(x+4)][(x+2)(x+3)]=120,即(x2+5x+4)(x2+5x+6)=120,设x2+5x+4=y,解关于y的一元二次方程求出y值,代入x2+5x+4=y,解两个一元二次方程即可得答案.
=0,去分母后可得y=9x或y=﹣5x,代入x2+2x﹣8=y,解两个一元二次方程即可得答案;(3)根据题意可得[(x+1)(x+4)][(x+2)(x+3)]=120,即(x2+5x+4)(x2+5x+6)=120,设x2+5x+4=y,解关于y的一元二次方程求出y值,代入x2+5x+4=y,解两个一元二次方程即可得答案.
(1)原方程可变形为![]() +1+
+1+![]() =
=![]() ,
,
令y=![]() ,则原方程可变为y+
,则原方程可变为y+![]() =
=![]() ,
,
解得y1=![]() ,y2=
,y2=![]() .
.
当y1=![]() 时,
时,![]() =
=![]() ,解得x=1;
,解得x=1;
当y2=![]() 时,
时,![]() =
=![]() ,解得x=
,解得x=![]() .
.
经检验:x=1或![]() 都是原方程的解.
都是原方程的解.
故原方程的解为x1=1,x2=![]() ,x3=
,x3=![]() .
.
(2)设x2+2x﹣8=y,则原方程可化为:![]() +
+![]() +
+![]() =0,
=0,
方程的两边同乘y(y+9x)(y﹣15x),整理得y2﹣4xy﹣45x2=0,
解得y=9x或y=﹣5x.
当y=9x时,x2+2x﹣8=9x,x2﹣7x﹣8=0,解得x1=8,x2=﹣1;
当y=﹣5x时,x2+2x﹣8=﹣5x,x2+7x﹣8=0,解得x3=﹣8,x4=1.
经检验:x1=8,x2=﹣1,x3=﹣8,x4=1都是原方程的解.
故原方程的解为x1=8,x2=﹣1,x3=﹣8,x4=1.
(3)[(x+1)(x+4)][(x+2)(x+3)]=120,
(x2+5x+4)(x2+5x+6)=120,
设x2+5x+4=y,则y(y+2)=120,
∴y2+2y﹣120=0,
解得y=10或y=﹣12.
当y=10时,x2+5x+4=10,x2+5x﹣6=0,解得x1=﹣6,x2=1;
当y=﹣12时,x2+5x+4=﹣12,x2+5x+16=0,△=25﹣64=﹣39<0,故此方程无实根.
故原方程的解为x1=﹣6,x2=1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,有“抛物线系”y=-(x-m)2+4m-3,顶点为点P,这些抛物线的形状与抛物线 y=-x2 相同,但顶点位置不同.
(1)填写下表,并说出:在m取不同数值时,点P位置的变化具有什么特征?
m的值 | … | -1 | 0 | 1 | 2 | … |
点P坐标 | … | … |
(2)若抛物线的对称轴是直线x=1,则可确定m的值.点M(p,q)为此抛物线上的一个动点,且﹣1<p<2,而直线y=kx-4(k≠0)始终经过点M.
①求此抛物线与x轴的交点坐标;
②求k的取值范围.
(3)若点Q在x轴上,点S(0,-1)在y轴上,点R在坐标平面内,且以点P,Q,R,S为顶点的四边形是正方形,试直接写出所有点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() ,点D是线段BC上的一动点,连接AD,过点D作
,点D是线段BC上的一动点,连接AD,过点D作![]() ,垂足为D,交射线AC与点
,垂足为D,交射线AC与点![]() 设BD为xcm,CE为ycm.
设BD为xcm,CE为ycm.
小聪根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小聪的探究过程,请补充完整:
![]() 通过取点、画图、测量,得到了x与y的几组值,如下表:
通过取点、画图、测量,得到了x与y的几组值,如下表:
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
|
|
|
| ___ |
| 0 |
|
|
|
| 0 |
![]() 说明:补全表格上相关数值保留一位小数
说明:补全表格上相关数值保留一位小数![]()
![]() 建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
![]() 结合画出的函数图象,解决问题:当线段BD是线段CE长的2倍时,BD的长度约为_____cm.
结合画出的函数图象,解决问题:当线段BD是线段CE长的2倍时,BD的长度约为_____cm.
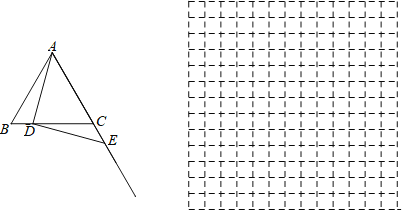
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y=![]() 的图象相交于点P1,P2,P3,P4,…Pn,再分别过P2,P3,P4,…Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,…,Bn﹣1,连接P1P2,P2P3,P3P4,…,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为_____.
的图象相交于点P1,P2,P3,P4,…Pn,再分别过P2,P3,P4,…Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,…,Bn﹣1,连接P1P2,P2P3,P3P4,…,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
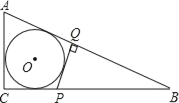
【题目】如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )
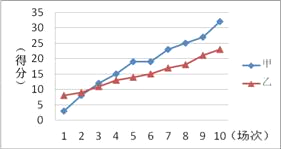
A. 甲运动员得分的平均数小于乙运动员得分的平均数B. 甲运动员得分的中位数小于乙运动员得分的中位数
C. 甲运动员得分的最小值大于乙运动员得分的最小值D. 甲运动员得分的方差大于乙运动员得分的方差
查看答案和解析>>
科目:初中数学 来源: 题型:
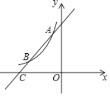
【题目】已知一次函数y=x+4图象与反比例函数y=![]() (k≠0)图象交于A(﹣1,a),B两点.
(k≠0)图象交于A(﹣1,a),B两点.
(1)求此反比例函数的表达式;
(2)若x+4≥![]() ,利用函数图象求x的取值范围.
,利用函数图象求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
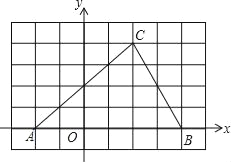
【题目】如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)
(2)若点C的坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , ),S△A′B′C′:S△ABC= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com