
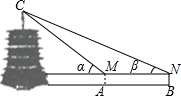
 星期天,身高为1.6米的小红、小涛来到一个公园,用他们所学的知识测算一座塔的高度.如图,小红站在A处测得她看塔顶C的仰角α为45°,小涛站在B处测得塔顶C的仰角β为30°,他们又测出A、B两点的距离为41.5米,假设他们的眼睛离头顶都是10厘米,求塔高(结果保留根号).
星期天,身高为1.6米的小红、小涛来到一个公园,用他们所学的知识测算一座塔的高度.如图,小红站在A处测得她看塔顶C的仰角α为45°,小涛站在B处测得塔顶C的仰角β为30°,他们又测出A、B两点的距离为41.5米,假设他们的眼睛离头顶都是10厘米,求塔高(结果保留根号). 分析 利用锐角三角函数关系得出PM的长,再利用$\frac{CP}{PN}$=tan30°,求出x的值即可.
解答 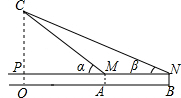 解:设塔底面中心为O,塔高xm,MN∥AB与塔中轴线相交于点P,得到△CPM、△CPN是直角三角形,
解:设塔底面中心为O,塔高xm,MN∥AB与塔中轴线相交于点P,得到△CPM、△CPN是直角三角形,
则$\frac{x-(1.6-0.1)}{PM}$=tan45°,
∵tan45°=1,
∴x-1.5=PM=CP,
在Rt△CPN中,$\frac{CP}{PN}$=tan30°,即$\frac{x-1.5}{x-1.5+41.5}$=$\frac{\sqrt{3}}{3}$,
解得:x=$\frac{83\sqrt{3}+89}{4}$.
答:塔高为$\frac{83\sqrt{3}+89}{4}$m.
点评 此题主要考查了解直角三角性的应用,根据题意熟练应用锐角三角函数关系是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
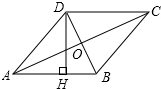 如图,四边形ABCD是菱形,对角线AC=8cm,DB=6cm,DH⊥AB于点H,则DH的长为( )
如图,四边形ABCD是菱形,对角线AC=8cm,DB=6cm,DH⊥AB于点H,则DH的长为( )| A. | 5cm | B. | 10cm | C. | $\frac{24}{5}$cm | D. | $\frac{48}{5}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com