
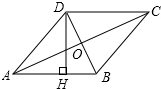
 如图,四边形ABCD是菱形,对角线AC=8cm,DB=6cm,DH⊥AB于点H,则DH的长为( )
如图,四边形ABCD是菱形,对角线AC=8cm,DB=6cm,DH⊥AB于点H,则DH的长为( )| A. | 5cm | B. | 10cm | C. | $\frac{24}{5}$cm | D. | $\frac{48}{5}$cm |
分析 先由勾股定理求出AB,再根据菱形面积的计算方法即可求出结果.
解答 解:∵四边形ABCD是菱形,
∴OA=$\frac{1}{2}$AC=4,OB=$\frac{1}{2}$BD=3,AC⊥BD,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵菱形ABCD的面积=AB•DH=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×8×6=24,
∴DH=$\frac{24}{5}$;
故选:C.
点评 本题考查了菱形的性质、面积的计算方法以及勾股定理的运用;熟练掌握菱形的性质和面积的计算方法进行计算是解决问题的关键.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
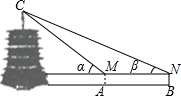 星期天,身高为1.6米的小红、小涛来到一个公园,用他们所学的知识测算一座塔的高度.如图,小红站在A处测得她看塔顶C的仰角α为45°,小涛站在B处测得塔顶C的仰角β为30°,他们又测出A、B两点的距离为41.5米,假设他们的眼睛离头顶都是10厘米,求塔高(结果保留根号).
星期天,身高为1.6米的小红、小涛来到一个公园,用他们所学的知识测算一座塔的高度.如图,小红站在A处测得她看塔顶C的仰角α为45°,小涛站在B处测得塔顶C的仰角β为30°,他们又测出A、B两点的距离为41.5米,假设他们的眼睛离头顶都是10厘米,求塔高(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
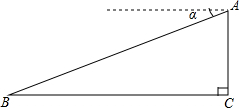 在寻找马航MH730航班的过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,从飞机上看目标B的俯角为α,此时飞机的飞行高度AC=1200米,tanα=$\frac{5}{12}$,则飞机距离疑似目标B的距离AB为( )
在寻找马航MH730航班的过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,从飞机上看目标B的俯角为α,此时飞机的飞行高度AC=1200米,tanα=$\frac{5}{12}$,则飞机距离疑似目标B的距离AB为( )| A. | 3120米 | B. | 2800$\sqrt{3}$米 | C. | 3260米 | D. | 3000$\sqrt{3}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-2+\sqrt{2}$ | B. | $-1+\sqrt{2}$ | C. | $3-\sqrt{2}$ | D. | $-2-\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com