
分析 (1)比较-x2+1与2的大小,得到答案;
(2)根据题意-x2-2x+k<-3,变形成k<x2+2x-3,由x2+2x-3=(x+1)2-4,可知当x=-1,x2+2x-3的最小值为-4,即可确定k的取值范围;
(3)根据当-1≤x≤2时,y=x2-x-6的值小于y=m(x-1)的值,解答即可.
解答 解:(1)∵-x2≤0,
∴-x2+1≤1,
∴-x2+1<2.
∴max{-x2+1,2}=2,
(2)∵max{-x2-2x+k,-3}=-3,
∴-x2-2x+k≤-3.
∴k≤x2+2x-3,
∵x2+2x-3=(x+1)2-4,
∴当x=-1,x2+2x-3的最小值为-4,
∴k≥-4;
(3)对于y=x2-x-6,当x=-1时,y=-4,
当x=2时,y=-4,
由题意可知抛物线y=x2-x-6与直线y=m(x-1)的交点坐标为(-1,-4),(2,-4),
所以m的范围是:-4≤m≤2.
点评 本题考查的是与二次函数和一次函数有关的新定义,根据题意理解新定义的计算公式是解题的关键,注意:一次函数和二次函数的性质的运用.


科目:初中数学 来源: 题型:解答题
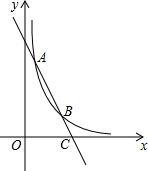 如图,已知一次函数y=kx+b与反比例函数的图象交于点A(m,6)和B(2,3).
如图,已知一次函数y=kx+b与反比例函数的图象交于点A(m,6)和B(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
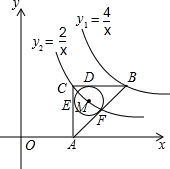 如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=$\frac{4}{x}$的图象经过点B;反比例函数y2=$\frac{2}{x}$的图象经过点C($\sqrt{2}$,m).
如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=$\frac{4}{x}$的图象经过点B;反比例函数y2=$\frac{2}{x}$的图象经过点C($\sqrt{2}$,m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
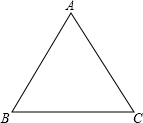 某新建小区要在一块的公共区修建一个圆形花坛,若要使花坛的面积最大,请你在这块区域内画出这个圆形花坛(使用直尺和圆规,不写画法,保留作图痕迹).
某新建小区要在一块的公共区修建一个圆形花坛,若要使花坛的面积最大,请你在这块区域内画出这个圆形花坛(使用直尺和圆规,不写画法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com