
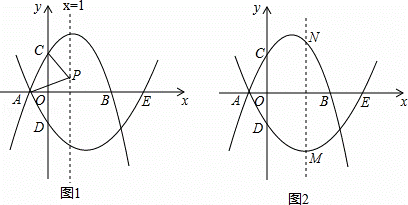
已知:抛物线l1:y=﹣x2+bx+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣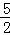 ).
).
(1)求抛物线l2的函数表达式;
(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标;
(3)M为抛物线l2上一动点,过点M作直线MN∥y轴,交抛物线l1 于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.
于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.
解:(1)∵抛物线l1:y=﹣x2+bx+3的对称轴为x=1,
∴﹣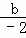 =1,解得b=2,
=1,解得b=2,
∴抛物线l1的解析式为y=﹣x2+2x+3,
令y=0,可得﹣x2+2x+3=0,解得x=﹣1或x=3,
∴A点坐标为(﹣1,0),
∵抛物线l2经过点A、E两点,
∴可设抛物线l2解析式为y=a(x+1)(x﹣5),
又∵抛物线l2交y轴于点D(0,﹣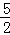 ),
),
∴﹣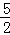 =﹣5a,解得a=
=﹣5a,解得a=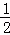 ,
,
∴y=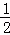 (x+1)(x﹣5)=
(x+1)(x﹣5)=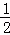 x2﹣2x﹣
x2﹣2x﹣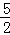 ,
,
∴抛物线l2的函数表达式为y= x2﹣2x﹣
x2﹣2x﹣ ;
;
(2)设P点坐标为(1,y),由(1)可得C点坐标为(0,3),
∴PC2=12+(y﹣3)2=y2﹣6y+10,PA2=[1﹣(﹣1)]2+y2=y2+4,
∵PC=PA,
∴y2﹣6y+10=y2+4,解得y=1,
∴P点坐标为(1,1);
(3)由题意可设M(x, x2﹣2x﹣
x2﹣2x﹣ ),
),
∵MN∥y轴,
∴N(x,﹣x2+2x+3), x2﹣2x﹣
x2﹣2x﹣
令﹣x2+2x+3= x2﹣2x﹣
x2﹣2x﹣ ,可解得x=﹣1或x=
,可解得x=﹣1或x=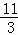 ,
,
①当﹣1<x≤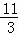 时,MN=(﹣x2+2x+3)﹣(
时,MN=(﹣x2+2x+3)﹣(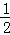 x2﹣2x﹣
x2﹣2x﹣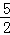 )=﹣
)=﹣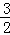 x2+4x+
x2+4x+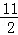 =﹣
=﹣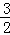 (x﹣
(x﹣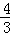 )2+
)2+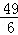 ,
,
显然﹣1<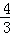 ≤
≤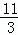 ,∴当x=
,∴当x=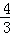 时,MN有最大值
时,MN有最大值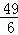 ;
;
②当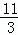 <x≤5时,MN=(
<x≤5时,MN=(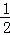 x2﹣2x﹣
x2﹣2x﹣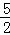 )﹣(﹣x2+2x+3)=
)﹣(﹣x2+2x+3)=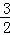 x2﹣4x﹣
x2﹣4x﹣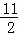 =
=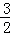 (x﹣
(x﹣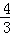 )2﹣
)2﹣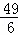 ,
,
显然当x>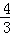 时,MN随x的增大而增大,
时,MN随x的增大而增大,
∴当x=5时,MN有最大值,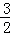 ×(5﹣
×(5﹣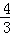 )2﹣
)2﹣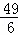 =12;
=12;
综上可知在点M自点A运动至点E的过程中,线段MN长度的最大值为12.


科目:初中数学 来源: 题型:
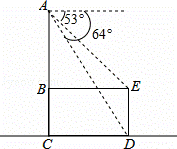
如图是放在水平地面上的一把椅子的侧面图,椅子高为AC,椅面宽为BE,椅脚高为ED,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得点D、E的俯角分别为64°和53°.已知ED=35cm,求椅子高AC约为多少?
(参考数据:tan53°≈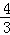 ,sin53°≈
,sin53°≈ ,tan64°≈2,sin64°≈
,tan64°≈2,sin64°≈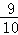 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
某学校为了推动球类运动的普及,成立多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题:
(1)本次抽样调查,共调查了 400 名学生;
(2)请将条形统计图和扇形统计图补充完整;
(3)若该学校共有学生1800人,根据以上数据分析,试估计选择排球运动的同学约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )
A. 70° B. 80° C. 110° D. 120°
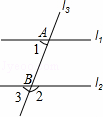
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com