
已知∠AOB内部有三条射线,其中OE平分∠BOC,OF平分∠AOC.
(1)如图1,若∠AOB=90°,∠AOC=30°,求EOF的度数;
(2)如图2,若∠AOB=α,求∠EOF的度数(用含α的式子表示);
(3)若将题中的“OE平分∠BOC,OF平分∠AOC”的条件改为“∠EOB=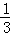 ∠BOC,∠COF=
∠BOC,∠COF= ∠AOC”,且∠AOB=α,求∠EOF的度数(用含α的式子表示)
∠AOC”,且∠AOB=α,求∠EOF的度数(用含α的式子表示)

【考点】角的计算;角平分线的定义.
【分析】(1)首先求得∠BOC的度数,然后根据角的平分线的定义和角的和差可得∠EOF=∠EOC+∠COF即可求解;
(2)根据角的平分线的定义和角的和差可得∠EOF=∠EOC+∠COF= ∠BOC+
∠BOC+ ∠AOC=
∠AOC= (∠BOC+∠AOC),即可求解;
(∠BOC+∠AOC),即可求解;
(3)根据角的等分线的定义可得∠EOF=∠EOC+∠COF= ∠BOC+
∠BOC+ ∠AOC=
∠AOC= (∠BOC+∠AOC)=
(∠BOC+∠AOC)= ∠AOB,即可求解.
∠AOB,即可求解.
【解答】解:(1)∠BOC=∠AOB﹣∠AOC=90°﹣30°=60°,
∵OE平分∠BOC,OF平分∠AOC,
∴∠EOC= ∠BOC=
∠BOC= ×60°=30°,∠COF=
×60°=30°,∠COF= ∠AOC=
∠AOC= ×30°=15°,
×30°=15°,
∴∠EOF=∠EOC+∠COF=30°+15°=45°;
(2)∵OE平分∠BOC,OF平分∠AOC,
∴∠EOC= ∠BOC,∠COF=
∠BOC,∠COF= ∠AOC,
∠AOC,
∴∠EOF=∠EOC+∠COF= ∠BOC+
∠BOC+ ∠AOC=
∠AOC= (∠BOC+∠AOC)=
(∠BOC+∠AOC)= ∠AOB=
∠AOB= a;
a;
(3)∵∠EOB=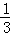 ∠BOC,
∠BOC,
∴∠EOC= ∠BOC,
∠BOC,
又∵∠COF= ∠AOC,
∠AOC,
∴∠EOF=∠EOC+∠COF= ∠BOC+
∠BOC+ ∠AOC=
∠AOC= (∠BOC+∠AOC)=
(∠BOC+∠AOC)= ∠AOB=
∠AOB= a.
a.
【点评】本题考查了角度的计算,理解角的平分线的定义以及角度的和、差之间的关系是关键.


科目:初中数学 来源: 题型:
如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是( )
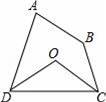

A.110° B.100° C.90° D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
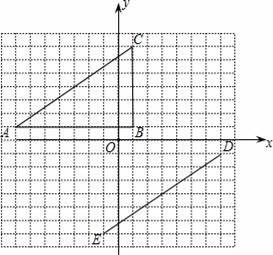
在平面直角坐标系中,△ABC的顶点坐标是A(﹣7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,﹣1),E(﹣1,﹣7).
(1)试说明如何平移线段AC,使其与线段ED重合;
(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°,画出旋转后的图形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com