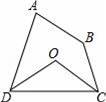
如图，四边形ABCD中，∠A+∠B=200°，∠ADC、∠DCB的平分线相交于点O，则∠COD的度数是（ ）
A．110° B．100° C．90° D．80°
B【考点】多边形内角与外角；三角形内角和定理．
【分析】由于∠A+∠B=200°，根据四边形的内角和定理求出∠ADC+∠DCB的度数，然后根据角平分线的定义得出∠ODC+∠OCD的度数，最后根据三角形内角和定理求出∠COD的度数．
【解答】解：∵∠A+∠B+∠ADC+∠DCB=360°，∠A+∠B=200°，
∴∠ADC+∠DCB=160°．
又∵∠ADC、∠DCB的平分线相交于点O，
∴∠ODC=
∠ADC，∠OCD=，
∴∠ODC+∠OCD=80°，
∴∠COD=180°﹣（∠ODC+∠OCD）=100°．
故选B．
【点评】本题主要考查了三角形及四边形的内角和定理．三角形的内角和等于180°，四边形的内角和等于360°
一线名师提优试卷系列答案科目：初中数学 来源： 题型：
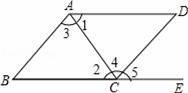
．如图，下列条件中：
（1）∠B+∠BCD=180°；
（2）∠1=∠2；
（3）∠3=∠4；
（4）∠B=∠5．
能判定AB∥CD的条件个数有（ ）
A．1 B．2 C．3 D．4
查看答案和解析>>
科目：初中数学 来源： 题型：
在“庆祝建党90周年的红歌传唱活动”比寒中，七位评委给某参赛队打的分数为：92、86、88、87、92、94、86，则去掉一个最高分和一个最低分后，所剩五个分数的平均数和中位数是（ ）
A．89，92 B．87，88 C．89，88 D．88，92
查看答案和解析>>
科目：初中数学 来源： 题型：
已知∠AOB内部有三条射线，其中OE平分∠BOC，OF平分∠AOC．
（1）如图1，若∠AOB=90°，∠AOC=30°，求EOF的度数；
（2）如图2，若∠AOB=α，求∠EOF的度数（用含α的式子表示）；
（3）若将题中的“OE平分∠BOC，OF平分∠AOC”的条件改为“∠EOB=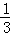
∠BOC，∠COF=
∠AOC”，且∠AOB=α，求∠EOF的度数（用含α的式子表示）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com