
.如图,下列条件中:
(1)∠B+∠BCD=180°;
(2)∠1=∠2;
(3)∠3=∠4;
(4)∠B=∠5.
能判定AB∥CD的条件个数有( )
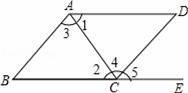

A.1 B.2 C.3 D.4
C【考点】平行线的判定.
【分析】根据平行线的判定定理,(1)(3)(4)能判定AB∥CD.
【解答】解:(1)∠B+∠BCD=180°,同旁内角互补,两直线平行,则能判定AB∥CD;
(2)∠1=∠2,但∠1,∠2不是截AB、CD所得的内错角,所不能判定AB∥CD;
(3)∠3=∠4,内错角相等,两直线平行,则能判定AB∥CD;
(4)∠B=∠5,同位角相等,两直线平行,则能判定AB∥CD.
满足条件的有(1),(3),(4).
故选:C.
【点评】本题考查了两直线平行的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行,并要分清给出的角所截的是哪两条直线.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )
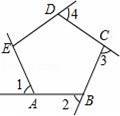

A.80° B.100° C.108° D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:
152=1×2×100+25=225,
252=2×3×100+25=625,
352=3×4×100+25=1225,
…
(1)根据上述格式反应出的规律填空:952= 5 ,
(2)设这类等式左边两位数的十位数字为a,请用一个含a的代数式表示其结果 ,
(3)这种简便计算也可以推广应用:
①个位数字是5的三位数的平方,请写出1952的简便计算过程及结果,
②十位数字相同,且个位数字之和是10的两个两位数想成的算式,请写出89×81的简便计算过程和结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是( )
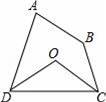

A.110° B.100° C.90° D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
据调查,某市2011年的房价为4000元/m2,预计2013年将达到4840元/m2,求这两年的年平均增长率,设年平均增长率为x,根据题意,所列方程为( )
A.4000(1+x)=4840 B.4000(1+x)2=4840
C.4000(1﹣x)=4840 D.4000(1﹣x)2=4840
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com