
 如图,已知点B,C分别在射线AN,AM上,∠MCB与∠NBC的平分线交于点P.
如图,已知点B,C分别在射线AN,AM上,∠MCB与∠NBC的平分线交于点P.| 2 |
| ||
| 2 |
 (1)证明:过点P作PD⊥AM,PF⊥AN,PE⊥BC,垂足分别为D、F、E,
(1)证明:过点P作PD⊥AM,PF⊥AN,PE⊥BC,垂足分别为D、F、E,
| ||
| 2 |
| PB2-PF2 |
| 52-42 |
| AF2+PF2 |
| 102+42 |
| 29 |


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
 如图,线段AC、BD交于点M,过B、D两点分别作AC的垂线段BF、DE,
如图,线段AC、BD交于点M,过B、D两点分别作AC的垂线段BF、DE,查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF长的最小值是
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF长的最小值是查看答案和解析>>
科目:初中数学 来源: 题型:
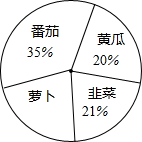 阿姨在一块蔬菜地里种植了4种不同的蔬菜,各种蔬菜的种植面积分布如图.
阿姨在一块蔬菜地里种植了4种不同的蔬菜,各种蔬菜的种植面积分布如图.| 品种 | 合计 | 黄瓜 | 韭菜 | 萝卜 | 番茄 |
| 种植面积/平方米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,∠C=90°,∠BAC=60°,AC=1,点D在BC上,点E在AB上,使得△ADE是等腰直角三角形,∠ADE=90°,求BE的长.(提示:可以运用“直角三角形中,30°角所对的直角边等于斜边的一半”).
如图,在△ABC中,∠C=90°,∠BAC=60°,AC=1,点D在BC上,点E在AB上,使得△ADE是等腰直角三角形,∠ADE=90°,求BE的长.(提示:可以运用“直角三角形中,30°角所对的直角边等于斜边的一半”).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com