
如图(1),E是正方形ABCD的边BC上的一个点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE;过点F作FG⊥BC交BC的延长线于点G.
(1)求证:FG=BE;
(2)连接CF,如图(2),求证:CF平分∠DCG;
(3)当 时,求sin∠CFE的值.
时,求sin∠CFE的值.

(1)证明见解析;(2)证明见解析;(3) .
.
【解析】
试题分析:(1)根据同角的余角相等得到一对角相等,再由一对直角相等,且AE=EF,利用AAS得到三角形ABE与三角形EFG全等,利用全等三角形的对应边相等即可得证.
(2)由(1)得到BC=AB=EG,利用等式的性质得到BE=CG,根据FG=BE,等量代价得到FG=CG,即三角形FCG为等腰直角三角形,得到∠FCG=45°,即可得证.
(3)如答图,作CH⊥EF于H,则△EHC∽△EGF,利用相似得比例,根据BE与BC的比值,设出BE,EC,以及EG,FG,利用勾股定理表示出EF,CF,进而表示出HC,在直角三角形HC中,利用锐角三角函数定义即可求出sin∠CFE的值.
试题解析:【解析】
(1)证明:∵EP⊥AE,∴∠AEB+∠GEF=90°.
又∵∠AEB+∠BAE=90°,∴∠GEF=∠BAE.
又∵FG⊥BC,∴∠ABE=∠EGF=90°.
在△ABE与△EGF中,∵ ,
,
∴△ABE≌△EGF(AAS).∴FG=BE.
(2)证明:由(1)知:BC=AB=EG,∴BC﹣EC=EG﹣EC. ∴BE=CG.
又∵FG=BE,∴FG=CG.
又∵∠CGF=90°,∴∠FCG=45°= ∠DCG .
∠DCG .
∴CF平分∠DCG .
(3)如答图,过点C作CH⊥EF于点H,
∵∠HEC=∠GEF,∠CHE=∠FGE=90°,
∴△EHC∽△EGF. ∴ .
.
∵ ,∴可设BE=3a,则EC=3a,EG=4a,FG=CG=3a,
,∴可设BE=3a,则EC=3a,EG=4a,FG=CG=3a,
∴EF=5a,CF= a.
a.
∴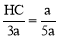 ,即HC=
,即HC= a.
a.
∴sin∠CFE= .
.

考点:1.四边形综合题;2. 正方形的性质;3.全等三角形的判定和性质;4. 等腰直角三角形的判定和性质;5.相似三角形的判定和性质;6. 锐角三角函数定义.


科目:初中数学 来源:2014年初中毕业升学考试(广西崇左卷)数学(解析版) 题型:选择题
如图,直线AB∥CD,如果∠1=70°,那么∠BOF的度数是( )

A.70° B.100° C.110° D.120°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西南宁卷)数学(解析版) 题型:选择题
如图,在 ABCD 中,点E是AD的中点,延长BC到点F,使CF : BC=1 : 2,连接DF,EC.若AB=5,AD=8,sinB=
ABCD 中,点E是AD的中点,延长BC到点F,使CF : BC=1 : 2,连接DF,EC.若AB=5,AD=8,sinB= ,则DF的长等于 ( )
,则DF的长等于 ( )

(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西南宁卷)数学(解析版) 题型:选择题
要使二次根式 在实数范围内有意义,则实数
在实数范围内有意义,则实数 的取值范围是 ( )
的取值范围是 ( )
(A) >
> (B)
(B) ≥
≥ (C)
(C) >
> (D)
(D) ≥
≥
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东汕尾卷)数学(解析版) 题型:解答题
一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3.从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com