
【题目】如图是放在地面上的一个长方体盒子,其中![]() ,在线段
,在线段![]() 的三等分点
的三等分点![]() (
(![]() E=3)处有一只蚂蚁,
E=3)处有一只蚂蚁,![]() 中点
中点![]() 处有一米粒,则蚂蚁沿长方体表面爬到米粒处的最短距离为( )
处有一米粒,则蚂蚁沿长方体表面爬到米粒处的最短距离为( )

A.10
B.![]()
C.5+![]()
D.6+![]()
 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于点
轴于点![]() .
.
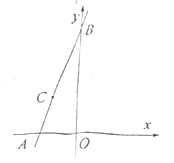
(1)当![]() ,自变量
,自变量![]() 的取值范围是 (直接写出结果);
的取值范围是 (直接写出结果);
(2)点![]() 在直线
在直线![]() 上.
上.
①直接写出![]() 的值为 ;
的值为 ;
②过![]() 点作
点作![]() 交
交![]() 轴于点
轴于点![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
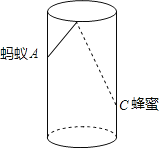
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一套西装送一条领带;②西装和领带都按定价的![]() 付款.
付款.
现某客户要到该服装厂购买西装20套,领带![]() 条(
条(![]() );
);
(1)若该客户按方案①购买,需付款____________________元(用含![]() 的代数式表示);若该客户按方案②购买,需付款__________________元(用含
的代数式表示);若该客户按方案②购买,需付款__________________元(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
(3)若![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
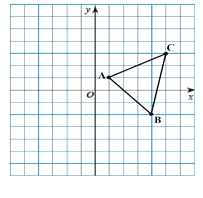
【题目】如图,在平面直角坐标系中, ABC 三个顶点的坐标分别为 A(1,1) , B(4, 2) ,C (5, 3) .
(1)在图中画出 ABC 关于 y 轴的对称 图形 A1B1C1 ;(要求:画出三角形,标出相应顶点的 字母,不写结论)
(2)分别写出A1B1C1 三个顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,同底数幂的乘法法则为:am·an=am+n(其中a≠0,m,n为正整数),类似地我们规定关于任意正整数m,n的一种新运算:h(m+n)=h(m)·h(n),请根据这种新运算填空:
(1)若h(1)=![]() ,则h(2)=________;
,则h(2)=________;
(2)若h(1)=k(k≠0),则h(n)·h(2017)=________(用含n和k的代数式表示,其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,画![]() ,并画
,并画![]() 的平分线
的平分线![]() .
.
(1)将三角尺的直角顶点落在![]() 的任意一点P上,使三角尺的两条直角边与
的任意一点P上,使三角尺的两条直角边与![]() 的两边分别垂直,垂足为E、F(如图1),则
的两边分别垂直,垂足为E、F(如图1),则![]()
![]() (选填<,>,=)
(选填<,>,=)

(2)把三角尺绕着点P旋转(如图2),![]() 与
与![]() 相等吗?试猜想
相等吗?试猜想![]() 、
、![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
拓展延伸1:在(2)条件下,过点P作直线![]() ,分别交
,分别交![]() 、
、![]() 于点G、H,如图3
于点G、H,如图3
①图中全等三角形有多少对(不添加辅助线)
②猜想![]() 、
、![]() 、
、![]() 之间的关系,并证明你的猜想.
之间的关系,并证明你的猜想.
拓展延伸2:
画![]() ,并画
,并画![]() 的平分线
的平分线![]() ,在
,在![]() 上任取一点P,作
上任取一点P,作![]() .
.![]() 的两边分别与
的两边分别与![]() 、
、![]() 相交于E、F两点(如图4),
相交于E、F两点(如图4),![]() 与
与![]() 相等吗?请说明理由.
相等吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com