
【题目】将![]() 旋转一定的角度后得到
旋转一定的角度后得到![]() ,如图所示,如果
,如图所示,如果![]() ,
,![]() .
.

![]() 指出其旋转中心和旋转的角度
指出其旋转中心和旋转的角度
![]() 求
求![]() 的长度;
的长度;
![]() 与
与![]() 的位置关系如何?说明理由.
的位置关系如何?说明理由.
【答案】![]() 点
点![]() 为旋转中心,对应边
为旋转中心,对应边![]() 、
、![]() 的夹角为旋转角即
的夹角为旋转角即![]() ;
;![]() ;(3)
;(3)![]() 、
、![]() 的位置关系为:
的位置关系为:![]() .理由见解析.
.理由见解析.
【解析】
(1)根据旋转的性质,点D为旋转中心,对应边BD、AD的夹角为旋转角;
(2)根据旋转的性质可得BD=AD,然后根据勾股定理计算即可;
(3)延长BE交AC于F,根据旋转可得△BDE和△ADC全等,根据全等三角形对应角相等可得∠DBE=∠DAC,然后求出∠DAC+∠AEF=90°,判断出BE⊥AC.
(1)由题意可知点D为旋转中心,对应边BD、AD的夹角为旋转角即90°;
(2)根据旋转的性质可得BD=AD=4cm,CD=2cm,∴AC=![]() =
=![]() =2
=2![]() cm;
cm;
(3)BE、AC的位置关系为:BE⊥AC.理由如下:
延长BE交AC于F.
∵△BDE按顺时针方向旋转一定角度后得到△ADC,∴△BDE≌△ADC,∴∠DBE=∠DAC.
∵∠DBE+∠BED=90°,∴∠DAC+∠AEF=90°,∴∠AFE=180°﹣90°=90°,∴BE⊥AC,∴BE、AC的位置关系为:BE⊥AC.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC分别沿AB,AC翻折得到△ABD 和△AEC,线段BD与AE交于点 F,连接BE .
(1)如果∠ABC=16,∠ACB=30°,求∠DAE的度数;
(2)如果BD⊥CE,求∠CAB 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点![]() ,在笔直的车道
,在笔直的车道![]() 上确定点
上确定点![]() ,使
,使![]() 和
和![]() 垂直,测得
垂直,测得![]() 的长等于
的长等于![]() 米,在
米,在![]() 上的同侧取点
上的同侧取点![]() 、
、![]() ,使
,使![]() ,
,![]() .
.

![]() 求
求![]() 、
、![]() 之间的路程(保留根号);
之间的路程(保留根号);
![]() 已知本路段对校车限速为
已知本路段对校车限速为![]() 米/秒若测得某校车从
米/秒若测得某校车从![]() 到
到![]() 用了
用了![]() 秒,这辆校车是否超速?请说明理由.
秒,这辆校车是否超速?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
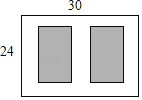
【题目】如图,某小区有一块长为30 m,宽为24 m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为________m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系的原点![]() 是正方形
是正方形![]() 的中心,顶点
的中心,顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,把正方形
,把正方形![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 得到正方形
得到正方形![]() ,则正方形
,则正方形![]() 与正方形
与正方形![]() 重叠部分形成的正八边形的边长为( )
重叠部分形成的正八边形的边长为( )

A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AD=5cm, AP=8cm , AP平分∠DAB,交DC于点P,过点B作BE⊥AD于点E,BE交AP于点F,则tan∠BFP= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海域有![]() 、
、![]() 、
、![]() 三艘船正在捕鱼作业,
三艘船正在捕鱼作业,![]() 船突然出现故障,向
船突然出现故障,向![]() 、
、![]() 两船发出紧急求救信号,此时
两船发出紧急求救信号,此时![]() 船位于
船位于![]() 船的北偏西
船的北偏西![]() 方向,距
方向,距![]() 船
船![]() 海里的海域,
海里的海域,![]() 船位于
船位于![]() 船的北偏东
船的北偏东![]() 方向,同时又位于
方向,同时又位于![]() 船的北偏东
船的北偏东![]() 方向.
方向.

(1)求![]() 的度数;
的度数;
![]() 船以每小时
船以每小时![]() 海里的速度前去救援,问多长时间能到出事地点.(结果精确到
海里的速度前去救援,问多长时间能到出事地点.(结果精确到![]() 小时).(参考数据:
小时).(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com