
【题目】如图,![]() ,
,![]() ,
,![]() ,…,是等腰直角三角形,点
,…,是等腰直角三角形,点![]() ,
,![]() ,
,![]() ,…,在反比例函数
,…,在反比例函数![]() 的图象上,斜边
的图象上,斜边![]() ,
,![]() ,
,![]() ,…都在
,…都在![]() 轴上,则点
轴上,则点![]() 的坐标是________.
的坐标是________.

【答案】![]()
【解析】
过点P1作P1M⊥x轴,由于△OA1P1是等腰直角三角形,因而P1A1=OA1,因而可以设P1点的坐标是(a,a),把(a,a)代入解析式即可求出a=2,因而求出P1的坐标是(2,2),进一步得到OA1=4,再根据△P2A1A2是等腰直角三角形,设P2的纵坐标是b,因而横坐标是b+ 4,把P2的坐标代入解析式![]() ,即可求出b,然后即可求出点B的坐标.
,即可求出b,然后即可求出点B的坐标.
如图,
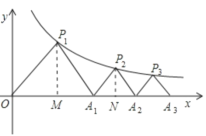
过点P1作P1M⊥x轴于M,∵△OA1P1是等腰直角三角形,∴P1M=OM,∴设P1点的坐标是(a,a),把(a,a)代入解析式![]() 得到a=2,∴P1的坐标是(2,2),则OA1=4,∵△P2A1A2是等腰直角三角形,过点P2作P2N⊥x轴于N,设P2的纵坐标是b,∴横坐标是b+4,把P2的坐标代入解析式
得到a=2,∴P1的坐标是(2,2),则OA1=4,∵△P2A1A2是等腰直角三角形,过点P2作P2N⊥x轴于N,设P2的纵坐标是b,∴横坐标是b+4,把P2的坐标代入解析式![]() 中,∴b+4=
中,∴b+4=![]() ,∴
,∴![]() ,∴点P2的横坐标为
,∴点P2的横坐标为![]() ,∴P2点的坐标是
,∴P2点的坐标是![]() ,∴点A2的坐标是
,∴点A2的坐标是![]() ,故答案为
,故答案为![]() .
.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,AA1,A1A2,A2A3,A3B,AB分别是五个半圆的直径,两只小虫同时出发,以相同的速度从点A到点B,甲虫沿ADA1,A1EA2,A2FA3,A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )

A. 甲先到点B B. 乙先到点B C. 甲、乙同时到点B D. 无法确定谁先到点B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是一座抛物线形拱桥,P 处有一照明灯,水面OA 宽4 m.从O,A 两处观测P 处,仰角分别为α,β,且tanα=![]() ,tanβ=
,tanβ=![]() .以O 为原点,OA 所在直线为x 轴建立平面直角坐标系.
.以O 为原点,OA 所在直线为x 轴建立平面直角坐标系.
(1)求点P的坐标;
(2)若水面上升1 m,则水面宽多少米(![]() 取1.41,结果精确到0.1 m)?
取1.41,结果精确到0.1 m)?

查看答案和解析>>
科目:初中数学 来源: 题型:
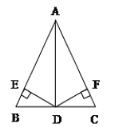
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.
(1)图中共有_________对全等三角形.
(2)求证:AD是△ABC的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(a2b﹣2ab2﹣b3)÷b﹣(a+b)(a﹣b),其中a=1,b=﹣2.
(2)先化简(1+![]() )÷
)÷![]() ,再从﹣1,0,1,2,3中选取一个合适的数作为x的值代入求值.
,再从﹣1,0,1,2,3中选取一个合适的数作为x的值代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,二次函数
,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,并过点
,并过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .抛物线
.抛物线![]() 和反比例函数
和反比例函数![]() 的图象都经过点
的图象都经过点![]() ,四边形
,四边形![]() 的面积是
的面积是![]() .
.
![]() 求反比例函数、二次函数的解析式及抛物线的对称轴;
求反比例函数、二次函数的解析式及抛物线的对称轴;
![]() 如图
如图![]() ,点
,点![]() 从
从![]() 点出发以每秒
点出发以每秒![]() 个单位的速度沿线段
个单位的速度沿线段![]() 向
向![]() 点运动,点
点运动,点![]() 从
从![]() 点出发以相同的速度沿线段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向
点出发以相同的速度沿线段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向![]() 点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为
点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为![]() 秒.
秒.
①当![]() 为何值时,四边形
为何值时,四边形![]() 为等腰梯形;
为等腰梯形;
②设![]() 与对称轴的交点为
与对称轴的交点为![]() ,过
,过![]() 点作
点作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,求面积
,求面积![]() 关于时间
关于时间![]() 的函数解析式,并指出
的函数解析式,并指出![]() 的取值范围;当
的取值范围;当![]() 为何值时,
为何值时,![]() 有最大值或最小值.
有最大值或最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为xm,面积为Sm2.

(1)求S与x的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45 m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com