
【题目】如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD,已知BC=BD,AB=4,BC=2![]() .
.
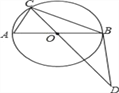
(1)求证:BD是⊙O的切线;
(2)求CD的长.
【答案】见解析
【解析】试题分析:(1)由AB为圆的直径,利用直径所对的圆周角为直角得到∠ACB为直角,进而得到三角形ABC为直角三角形,利用锐角三角函数定义求出sinA的值,利用特殊角的三角函数值求出∠A的度数为60度,再由OA=OC,得到三角形AOC为等边三角形,利用等边三角形的性质得到两个角为60度,进而求出∠BCD为30度,利用三角形内角和定理求出∠OBD为直角,即OB垂直于BD,即可得 证;
(2)由AB为直径,求出半径为2,由BC=BD,利用等边对等角得到一对角相等,再由OC=OB得到一对角相等,等量代换得到∠D=∠OBC,再由一对公共角相等,得到三角形OCB与三角形BCD相似由相似得比例,即可求出CD的长.
试题解析:(1)∵AB为圆O的直径,∴∠ACB=90°,在Rt△ABC中,∵sinA=![]() ,∴∠A=60°,∵AO=CO,∴△AOC为等边三角形,∴∠AOC=∠ACO=60°,∴∠BCD=∠ACB﹣∠ACO=90°﹣60°=30°,∵∠BOD=∠AOC=60°,∴∠OBD=180°﹣(∠BOD+∠D)=90°,∴OB ⊥BD,则BD为圆O的切线;
,∴∠A=60°,∵AO=CO,∴△AOC为等边三角形,∴∠AOC=∠ACO=60°,∴∠BCD=∠ACB﹣∠ACO=90°﹣60°=30°,∵∠BOD=∠AOC=60°,∴∠OBD=180°﹣(∠BOD+∠D)=90°,∴OB ⊥BD,则BD为圆O的切线;
(2)∵AB为圆O的直径,且AB=4,∴OB=OC=2,∵BC=BD,∴∠BCD=∠D,∵OC=OB,∴∠BCD=∠OBC,∴∠D=∠OBC,在△BCD和△OCB中,∠D=∠OBC,∠BCD=∠OCB,∴△BCD∽△OCB,∴![]() ,即
,即![]() ,则CD=6.
,则CD=6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列等式中,成立的是( )
A. (a+b)2=a2+b2B. (a-b)2=a2-b2
C. (-a+b)(a-b)=a2-b2D. (a-b)2=a2-2ab+b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列函数关系中,属于正比例函数关系的是( )
A.圆的面积与它的半径
B.面积为常数S时矩形的长y与宽x
C.路程是常数时,行驶的速度v与时间t
D.三角形的底边是常数a时它的面积S与这条边上的高h
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组数:1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,…其中每个数n都连续出现n次,那么这一组数的第119个数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com