
 在⊙O中,半径OA⊥OB,C是OB延长线上一点,AC交⊙O于点D.求证:∠AOD=2∠C.
在⊙O中,半径OA⊥OB,C是OB延长线上一点,AC交⊙O于点D.求证:∠AOD=2∠C. 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
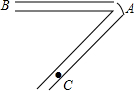 工人李师傅想制作一个如图所示的“V”形零件,他先把材料变成一个40°的锐角,然后准备在C处第二次加工拐弯,请你帮助他算一下,他应该怎样向外弯才能保证变过来的部分与AB保持平行?你的依据是什么?
工人李师傅想制作一个如图所示的“V”形零件,他先把材料变成一个40°的锐角,然后准备在C处第二次加工拐弯,请你帮助他算一下,他应该怎样向外弯才能保证变过来的部分与AB保持平行?你的依据是什么?查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ADE∽△ABC,AD=40,BD=20,BC=50,∠A=70°,∠ABC=30°.
如图,△ADE∽△ABC,AD=40,BD=20,BC=50,∠A=70°,∠ABC=30°.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com