【题目】如图，正方形ABCD和正方形OEFG中，点A和点F的坐标分别为 （3，2），（-1，-1），则两个正方形的位似中心的坐标是（ ）

A．（1，0）

B．（-5，-1）

C．（1，0）或（-5，-1）

D．（1，0）或（-5，-2）

参考答案：

【答案】D

【解析】

试题分析：考查位似变换中对应点的坐标的变化规律．本题应分两种情况讨论，一种是E和C是对应点，G和A是对应点；二种是A和E是对应点，C和G是对应点．

解：∵正方形ABCD和正方形OEFG中A和点F的坐标分别为（3，2），（﹣1，﹣1），

∴E（﹣1，0）、G（0，﹣1）、D（5，2）、B（3，0）、C（5，0），

（1）当E和C是对应顶点，G和A是对应顶点时，位似中心就是EC与AG的交点，

设AG所在直线的解析式为y=kx+b（k≠0），

∴，解得．

∴此函数的解析式为y=x﹣1，与EC的交点坐标是（1，0）；

（2）当A和E是对应顶点，C和G是对应顶点时，位似中心就是AE与CG的交点，

设AE所在直线的解析式为y=kx+b（k≠0），

，解得，故此一次函数的解析式为y=x+…①，

同理，设CG所在直线的解析式为y=kx+b（k≠0），

，解得，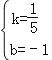

故此直线的解析式为y=x﹣1…②

联立①②得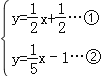

解得，故AE与CG的交点坐标是（﹣5，﹣2）．

故答案为：（1，0）、（﹣5，﹣2）．

关闭