
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:

学生最喜欢的节目人数条形统计图
节目 | 人数( 名 ) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 |
|
中国诗词大会 |
| 40% |
出彩中国人 | 10 | 20% |
学生最喜爱的节目人数统计表
根据以上提供的信息,解答下列问题:
(1)![]() =
= ![]() =
= ![]() = ;
= ;
(2)补全条形统计图;
(3)若该校共有学生1200名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名?
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
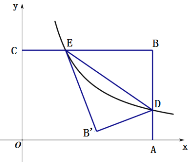
【题目】如图,平面直角坐标系xOy中,线段BC∥x轴、线段AB∥y轴,点B坐标为(4,3),反比例函数y=![]() (x>0)的图像与线段AB交于点D,与线段BC交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,则点B'的纵坐标是( )
(x>0)的图像与线段AB交于点D,与线段BC交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,则点B'的纵坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菜矿泉水厂在山脚下筑有水池蓄水,山泉水不停地流入水池,水池底部有大小两个排水口,
(1)当蓄水到![]() 吨时, 需要截住泉水清理水池。若开放小排水口
吨时, 需要截住泉水清理水池。若开放小排水口![]() 小时,再开放大排水口
小时,再开放大排水口![]() 分钟,能排完水池半的水:若同时开放两个排水口
分钟,能排完水池半的水:若同时开放两个排水口![]() 小时,刚好把水排完.求两个排水口每分钟的流量;
小时,刚好把水排完.求两个排水口每分钟的流量;
(2)现关闭排水口,开放泉水放满水池后,泉水仍以固定的流量流入水池.若用-台抽水机抽水,![]() 小时刚好把水抽完;若用
小时刚好把水抽完;若用![]() 台抽水机抽水,
台抽水机抽水,![]() 分钟刚好把水抽完。证明:抽水机每分针的抽水量是泉水流量的
分钟刚好把水抽完。证明:抽水机每分针的抽水量是泉水流量的![]() 倍;
倍;
(3)在![]() 的条件下,若用
的条件下,若用![]() 台抽水机抽水,需要名长时间刚好把水池的水抽完?
台抽水机抽水,需要名长时间刚好把水池的水抽完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)如图1,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,先将三角板的
,先将三角板的![]() 角与
角与![]() 重合,再将三角板绕点
重合,再将三角板绕点![]() 按顺时针方向旋转(旋转角大于
按顺时针方向旋转(旋转角大于![]() 且小于
且小于![]() ),旋转后三角板的一直角边与
),旋转后三角板的一直角边与![]() 交于点
交于点![]() .在三角板另一直角边上取一点
.在三角板另一直角边上取一点![]() ,使
,使![]() ,线段
,线段![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .
.

(1)请求出![]() 的度数?
的度数?
(2)![]() 与
与![]() 相等吗?请说明理由;
相等吗?请说明理由;
(类比探究)如图2,![]() 为等边三角形,先将三角板中的
为等边三角形,先将三角板中的![]() 角与
角与![]() 重合,再将三角板绕点
重合,再将三角板绕点![]() 按顺时针方向旋转(旋转角大于
按顺时针方向旋转(旋转角大于![]() 且小于
且小于![]() ).旋转后三角板的一直角边与
).旋转后三角板的一直角边与![]() 交于点
交于点![]() .在三角板斜边上取一点
.在三角板斜边上取一点![]() ,使
,使![]() ,线段
,线段![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .
.
(3)直接写出![]() _________度;
_________度;
(4)若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意两个数![]() 、
、![]() 的大小比较,有下面的方法:当
的大小比较,有下面的方法:当![]() 时,一定有
时,一定有![]() ;当
;当![]() 时,一定有
时,一定有![]() ;当
;当![]() 时,一定有
时,一定有![]() .反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.请根据以上材料完成下面的题目:
.反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.请根据以上材料完成下面的题目:
(1)已知:![]() ,
,![]() ,且
,且![]() ,试判断
,试判断![]() 的符号;
的符号;
(2)已知:![]() 、
、![]() 、
、![]() 为三角形的三边,比较
为三角形的三边,比较![]() 和
和![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,过点B做射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,连接DF,设运动的时间为t秒(t>0).

(1)当t为________时,AD=AB,此时DE的长度为________;
(2)当△DEF与△ACB全等时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.
①当t>![]() 时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
②当线段A′C′与射线BB1有公共点时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆半径,半径OC⊥AB于点O,点D是弧BC的中点,连接CD、AD、OD,给出以下四个结论:①∠DOB=∠ADC;②CE=OE;③△ODE∽△ADO;④2CD2=CE·AB.其中正确结论的序号是( )

A. ①③ B. ②④ C. ①④ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com