
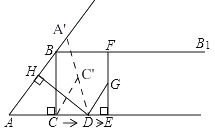
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=6��BC=8������B������BB1��AC������D�ӵ�A����������AC������ÿ��5����λ���ٶ��˶���ͬʱ����E�ӵ�C����������AC������ÿ��3����λ���ٶ��˶�������D��DH��AB��H������E��EF��AC������BB1��F������DF�����˶���ʱ��Ϊt�루t��0����

��1����tΪ________ʱ��AD=AB����ʱDE�ij���Ϊ________��
��2������DEF���ACBȫ��ʱ����t��ֵ��
��3����DH����ֱ��Ϊ�Գ��ᣬ�߶�AC����ԳƱ任���ͼ��ΪA��C�䣮
����t��![]() ʱ�����ADA�������ΪS��ֱ��д��S����t�ĺ�����ϵʽ��
ʱ�����ADA�������ΪS��ֱ��д��S����t�ĺ�����ϵʽ��
�����߶�A��C��������BB1�й�����ʱ����t��ȡֵ��Χ��
���𰸡���1��2��2����2��t=6����3����S=12t2���� ![]() .
.
�����������������(1)������Rt��ABC�Ĺ��ɶ������AB=10������AD=AB�ó�t��ֵ�������������CD�ij��ȣ�Ȼ�����DE=CE-CD����𰸣�(2)�����ȸ�������ó��ı���BCEFΪ���Σ��������������AD��AEʱ���t��ȡֵ��Χ��Ȼ����ݡ�ACB�͡�DEFȫ�ȵó�t��ֵ����AD��AEʱ���t��ȡֵ��Χ��Ȼ����ݡ�ACB�͡�DEFȫ�ȵó�t��ֵ��(3)����������ó���ABC�͡�ADH���ƣ��Ӷ��ó�AH=3t��DH=4t���Ӷ��ó���������ʽ������A'��������BB1�ϵĵ�Bʱ��AA'=AB=10������AA'=2AH=2��5t��cos��A�ó�t��ֵ������C'��������BB1��ʱ���ı���ACC'BΪƽ���ı��Σ�����CC'=2CD��cos��A���t��ֵ���Ӷ��ó�t��ȡֵ��Χ��
����������⣺��1����Rt��ABC�У�AC=6��BC=8�����ݹ��ɶ����ã�AB=![]() =10��
=10��
���˶�֪��AD=5t�� ��AD=AB�� ��5t=10�� ��t=2��
��CD=AD��AC=10��6=4��CE=3t=6�� ��DE=CE��CD=2��
(2)���⣺�ߡ�ACB=90�㣬BB1��AC��EF��AC�� ���ı���BCEF�Ǿ��Σ�EF=BC=8��
��AD��AEʱ��5t��6+3t�� ��0��t��3��
��DE=AC����ACB�ա�DEF��DE=AE��AD=6+3t��5t=6��2t�� ��6��2t=6�� ��t=0��
��t��0���������⣬�ᣩ��
��AD��AEʱ��5t��6+3t�� ��t��3��
��DE=AC����ACB�ա�DEF��DE=AD��AE=5t��6��3t=2t��6��
��2t��6=6�� ��t=6�� �൱t=6ʱ����DEF���ACBȫ�ȣ�
(3)���⣺����ͼ��
�ߡ�ACB=��AHD����BAC=��DAH�� ���ABC�ס�ADH�� ��![]() ��
��
��![]() �� ��AH=3t��DH=4t�� ��S��ADA'=2S��ADH=2��
�� ��AH=3t��DH=4t�� ��S��ADA'=2S��ADH=2��![]() AH��DH=AH��DH=12t2 ��
AH��DH=AH��DH=12t2 ��
������A'��������BB1�ϵĵ�Bʱ��AA'=AB=10��
��DH��AB�� ��AA'=2AH=2��5t��cos��A=6t=10�� ��t=![]() ��
��
����C'��������BB1��ʱ��CC'��AB�� ��BB1��AC�����ı���ACC'BΪƽ���ı��Σ�
��CC'=AB=10�� ��CC'=2CD��cos��A=2����5t��6����![]() =
=![]() ��5t��6���� ��t=
��5t��6���� ��t=![]() ��
��
��![]() ��t��
��t��![]() ���߶�A'C'������BB1�й����㣮
���߶�A'C'������BB1�й����㣮


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���֪AB=4��BC=3��������ֱ�����������½ǵĶ���B������ת90����ͼ��λ�ã��������½ǵĶ������������ת90����ͼ��λ�ã������Դ����ƣ�����������ת2016�κ���A��������ת��������������·��֮���ǣ�������

A. 2015�� B. 3019.5�� C. 3018�� D. 3024��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A����4��2����B��n����4��������һ�κ���y=kx+b�ͷ���������y=![]() ͼ����������㣮
ͼ����������㣮
��1����һ�κ����ͷ����������Ľ���ʽ��
��2������AOB�������
��3���۲�ͼ��ֱ��д������ʽkx+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���![]() �У�
��![]() ��
��![]() �ֱ�Ϊ��
�ֱ�Ϊ��![]() ��
��![]() ���е㣬
���е㣬![]() �ǶԽ��ߣ�����
�ǶԽ��ߣ�����![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��

��1����֤��![]() ��
��
��2����![]() ����֤���ı���
����֤���ı���![]() �����Σ�
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУѧ���ԡ���ǿ���ԡ������ʶ��ߡ������й�ʫ�ʴ�ᡷ���������й��ˡ��ĸ����ӽ�Ŀ��ϲ������������ȡ��![]() ��ѧ�����е���ͳ�ƣ�Ҫ��ÿ��ѧ��ѡ������ֻ��ѡ��һ���Լ���ϲ���Ľ�Ŀ�����������������Ƴ�����ͳ��ͼ��:
��ѧ�����е���ͳ�ƣ�Ҫ��ÿ��ѧ��ѡ������ֻ��ѡ��һ���Լ���ϲ���Ľ�Ŀ�����������������Ƴ�����ͳ��ͼ��:

ѧ����ϲ���Ľ�Ŀ��������ͳ��ͼ
��Ŀ | ����( �� ) | �ٷֱ� |
��ǿ���� | 5 | 10% |
�ʶ��� | 15 |
|
�й�ʫ�ʴ�� |
| 40% |
������� | 10 | 20% |
ѧ����ϲ���Ľ�Ŀ����ͳ�Ʊ�
���������ṩ����Ϣ�������������:
��1��![]() =
= ![]() =
= ![]() = ��
= ��
��2����ȫ����ͳ��ͼ��
��3������У����ѧ��1200�������ݳ��������������Ƹ�У��ϲ�����й�ʫ�ʴ�ᡷ��Ŀ��ѧ���ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
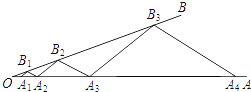
����Ŀ����ͼ����A1��A2������OA�ϣ�B1������OB�ϣ�������A2B2��A1B1 ��A3B2��A2B1 �� A3B3��A2B2 �� A4B3��A3B2 �� ��������A2B1B2����A3B2B3������ֱ�Ϊ1��9������A1007B1007A1008�������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵ�У���ABC�Ķ��㶼��������ϣ����У�C������Ϊ��1��2����
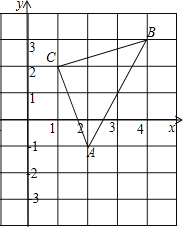
��1��д����A��B�����꣺A�� �� ����B�� �� ����
��2������ABC�������
��3������ABC������ƽ��2����λ���ȣ�������ƽ��1����λ���ȣ��õ���A��B��C�䣬������A��B��C�䣬д��A�䡢B�䡢C�����������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.Ϊ���˽�ij��ѧ![]() ��ѧ����������������������ȡ��
��ѧ����������������������ȡ��![]() ��ѧ�����е��飬�ڴ˴ε����У���������Ϊ
��ѧ�����е��飬�ڴ˴ε����У���������Ϊ![]() ��ѧ��������
��ѧ��������
B.��һ����Ϸ���н�����![]() ������
������![]() ����������Ϸһ�����н�
����������Ϸһ�����н�
C.�˽�������ÿ��������˿��������ó������鷽ʽ
D.����һöӲ�ң����泯�����DZ�Ȼ�¼�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�����Ϊ1����һ�β٣��ֱ��ӳ�AB��BC��CA����A1��B1��C1��ʹA1B��AB��B1C��BC��C1A��CA��˳������A1��B1��C1���õ���A1B1C1���ڶ��β������ֱ��ӳ�A1B1��B1C1��C1A1����A2��B2��C2��ʹA2B1��A1B1��B2C1��B1C1��C2A1��C1A1��˳������A2��B2��C2���õ���A2B2C2�������˹��ɣ�Ҫʹ�õ��������ε��������2016�����پ������������β�����

A.6B.5C.4D.3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com