练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．已知方程（2011x）2-（2010×2012）x-1-0的较大根为p，方程2010x2-2011x+1=0的较小根为q，求p-q的值．

    分析 先利用因式分解法分别解两个一元二次方程得到p和q的值，然后进行它们的差．

    解答 解：∵（2011x）2-（2010×2012）x-1=0
    ∴（20112x+1）（x-1）=0，
    ∴x1=-$\frac{1}{201{1}^{2}}$，x2=1，则p=1，
    2010x2-2011x+1=0，
    （2010x-1）（x-1）=0，
    ∴x1=$\frac{1}{2010}$，x2=1，则q=$\frac{1}{2010}$，
    ∴p-q=1-$\frac{1}{2010}$=$\frac{2009}{2010}$．

    点评 本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．也考查了因式分解法解一元二次方程．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．我市一家电子计算器专卖店，某型号计算器每只进价13元，售价20元，多买优惠：凡是一次买10只以上的，每多买1只，所买的全部计算器每只就降低0.10元，但是最低价为每只16元．例如，某人买20只计算器，于是每只降价0.10×（20-10）=1（元），因此，所买的全部20只计算器都按照每只19元计算．
    （1）求一次至少买多少只，才能以最低价购买？
    （2）写出该专卖店当一次销售x（只）时，所获利润y（元）与x（只）之间的函数关系式，并写出自变量x的取值范围；
    （3）若店主一次卖的只数在10至50只之间，问一次卖多少只获得的利润最大？其最大利润为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

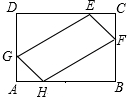    6．如图，在矩形ABCD中，AB=8，BC=4，点H、F、E、G分别在AB、BC、CD、DA上，且AH=AG=CE=CF=x，四边形EFHG的面积为y．
    （1）求y与x之间的函数关系式；
    （2）当x为何值时．四边形EFHG的面积最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知a、b、c是△ABC的三边．且a=2，b=5．
    （1）求第三边c的取值范围：
    （2）若三角形的周长是奇数．求c的值；
    （3）若第三边c为奇数，求c的取值．并判断此时△ABC的形状．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．把下列各式分母有理化：
    （1）$\frac{a-b}{\sqrt{a}+\sqrt{b}}（a≠b）$
    （2）$\frac{\sqrt{a+2}-\sqrt{a-2}}{\sqrt{a+2}+\sqrt{a-2}}$
    （3）$\frac{b-\sqrt{{a}^{2}+{b}^{2}}}{b+\sqrt{{a}^{2}+{b}^{2}}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．先阅读下面的材料．再解答下面的问题．
    ∵（$\sqrt{a}$+$\sqrt{b}$）（$\sqrt{a}$-$\sqrt{b}$）=a-b，
    ∴a-b=（$\sqrt{a}$+$\sqrt{b}$）（$\sqrt{a}$-$\sqrt{b}$）
    特别地．（$\sqrt{12}$+$\sqrt{11}$）×（$\sqrt{12}$-$\sqrt{11}$）=1，
    ∴$\frac{1}{\sqrt{12}-\sqrt{11}}$=$\sqrt{12}$+$\sqrt{11}$，
    当然也可以利用12-11=1得1=12-11，
    故$\frac{1}{\sqrt{12}-\sqrt{11}}$=$\frac{（\sqrt{12}）^2-（\sqrt{11}）^2}{\sqrt{12}-\sqrt{11}}$=$\sqrt{12}+\sqrt{11}$
    这种变形也是将分母有理化．
    利用上述的思路方法解答下列问题：
    （1）计算：$\frac{1}{3-\sqrt{8}}$-$\frac{1}{\sqrt{8}-\sqrt{7}}$+$\frac{1}{\sqrt{7}-\sqrt{6}}$-$\frac{1}{\sqrt{6}-\sqrt{5}}$+$\frac{1}{\sqrt{5}+2}$；
    （2）计算：$\frac{5}{4-\sqrt{11}}$-$\frac{4}{\sqrt{11}-\sqrt{7}}$-$\frac{2}{3+\sqrt{7}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．若y=$\sqrt{1-x}+\sqrt{x-1}+{x}^{2}-1$，你能求出2x-y的值吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知a=$\frac{1}{\sqrt{2}}$，求$\frac{1-2a+{a}^{2}}{a-1}$-$\frac{\sqrt{{a}^{2}-2a+1}}{{a}^{2}-a}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．（1）-2.4-（-3.5）+（-4.6）+3.5；　
    （2）（-2）2×5-（-2）3÷4．

    查看答案和解析>>

    同步练习册答案