
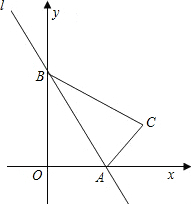
 如图,直线l:y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别相交于点A、B,△AOB与△ACB关于直线l对称,则∠OBC=60°.点C的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
如图,直线l:y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别相交于点A、B,△AOB与△ACB关于直线l对称,则∠OBC=60°.点C的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$). 分析 过点C作CE⊥x轴于点E,先根据直角三角形的性质求出OA,OB的长度,根据直角三角形特殊角的三角函数值可求得有关角的度数.利用轴对称性和直角三角函数值可求得AE,CE的长度,从而求得点C的坐标.
解答 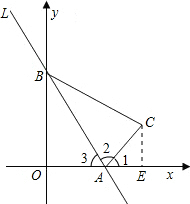 解:过点C作CE⊥x轴于点E,
解:过点C作CE⊥x轴于点E,
由直线AB的解析式可知
当x=0时,y=-$\sqrt{3}$x+$\sqrt{3}$,即OB=$\sqrt{3}$
当y=0时,x=1,即OA=1
∵∠AOB=∠C=90°,tan∠3=OB:OA=$\sqrt{3}$
∴∠3=60°,
∵△AOB与△ACB关于直线l对称
∴∠2=∠3=60°,则∠OBC=60°,AC=OA=1,
∴∠1=180°-∠2-∠3=60°,
在Rt△ACE中,
AE=cos60°×AC=$\frac{1}{2}$×1=$\frac{1}{2}$,
CE=sin60°×AC=$\frac{\sqrt{3}}{2}$,
∴OE=1+$\frac{1}{2}$=$\frac{3}{2}$,
∴点C的坐标是($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
故答案为:60°,($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
点评 本题主要考查了一次函数图象上点的性质和有关轴对称的性质,熟练运用数形结合的知识解题是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 东明县是鲁西南的化工基地,有东明石化集团,洪业化工集团,玉皇化工集团等企业,化学工业越来越成为东明县经济的命脉,化工厂里我们会经常看到如图储存罐,根据需要,在圆柱形罐的外围要安装小梯子,如果油罐的底面半径为6米,高24米,梯子绕罐体半圆到达罐顶,则梯子至少要多长?
东明县是鲁西南的化工基地,有东明石化集团,洪业化工集团,玉皇化工集团等企业,化学工业越来越成为东明县经济的命脉,化工厂里我们会经常看到如图储存罐,根据需要,在圆柱形罐的外围要安装小梯子,如果油罐的底面半径为6米,高24米,梯子绕罐体半圆到达罐顶,则梯子至少要多长?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25.51千克 | B. | 25.30千克 | C. | 24.80千克 | D. | 24.70千克 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -0.02克 | B. | +0.02克 | C. | 0克 | D. | +0.04克 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com