
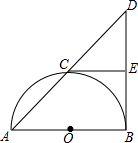
 如图,AB是半圆O的直径,EB、EC分别与半圆O相切于点B、C,连接AC并延长,与BE的延长线交于点D.
如图,AB是半圆O的直径,EB、EC分别与半圆O相切于点B、C,连接AC并延长,与BE的延长线交于点D.分析 (1)根据切线长定理证明EC=EB,然后根据等角对等边,证明ED=EB即可证得;
(2)首先证明∠ABC=∠D,在直角△ABC中利用三角函数的定义与勾股定理即可求解.
解答 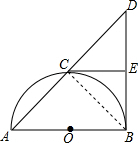 解:(1)连接BC.
解:(1)连接BC.
∵EB、EC分别与半圆O相切于点B、C,
∴EC=EB,
∴∠ECB=∠EBC,
∵AB是直径,
∴∠ACB=90°,
∴∠DCB=90°,即∠DCE+∠ECB=90°,
∴∠D+∠DBC=90°,
∴∠D=∠DCE,
∴DE=CE,
∴EB=ED;
(2)∵∠D+∠DBC=90°,∠BDC+∠ABC=90°,
∴∠ABC=∠D.
∴在直角△ABC中,cos∠ABC=cos∠D=$\frac{BC}{AB}$=$\frac{3}{5}$.
∴设BC=3x,则AB=5x,
∵直角△ABC中,AC2+BC2=AB2,即(3x)2+AC2=(5x)2,
解得x=2,
则AB=10.
则半圆O的半径是5.
点评 本题考查了切线长定理以及三角函数,正确证明ED=EC以及∠ABC=∠D是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
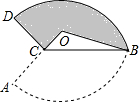 如图,扇形AOB的半径为2$\sqrt{3}$,圆心角为120°,C是半径OA上一点,将扇形OAB沿BC折叠使点A落在点D处.若DC⊥AC,图中阴影部分的面积为4$π+3\sqrt{3}-9$.
如图,扇形AOB的半径为2$\sqrt{3}$,圆心角为120°,C是半径OA上一点,将扇形OAB沿BC折叠使点A落在点D处.若DC⊥AC,图中阴影部分的面积为4$π+3\sqrt{3}-9$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
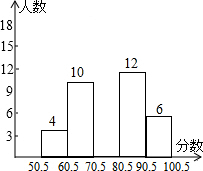 某班数学期末考试后,班主任将所得的成绩(分数取整数)进行整理分成5组,并绘成频数分布直方图(如图),已知70.5~80.5分数段的频率为0.36,请结合直方图提供的信息,解答以下问题:
某班数学期末考试后,班主任将所得的成绩(分数取整数)进行整理分成5组,并绘成频数分布直方图(如图),已知70.5~80.5分数段的频率为0.36,请结合直方图提供的信息,解答以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com