
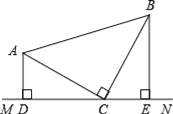
【题目】如图,在△ABC中∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)求证:△ADC≌△CEB;
(2)若AD=1,BE=2,求△ABC的面积.
【答案】见解析
【解析】
试题分析:
(1)如图,由已知易得在△ADC和△CEB中,AC=BC,∠ADC=∠CEB=90°,所有只需利用∠ACD+∠CAD=90°和∠ACD+∠BCE=90°,证得∠CAD=∠BCE就可以利用“角角边”证两三角形全等了;
(2)由(1)中结论:△ADC≌△CEB可得CE=AD=1,CD=BE=2,从而得到:DE=CD+CE=3,最后用梯形ABED的面积减去△ADC和△BCE的面积就可得到△ABC的面积.(学习“勾股定理”后也可利用“勾股定理”求得AC和BC的长直接计算△ABC的面积).
试题解析:
(1)证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°,
又∵AD⊥MN,BE⊥MN,∴∠ADC=∠CEB=90°,
而∠ACD+∠DAC=90°,∴∠BCE=∠CAD.
在△ADC和△CEB中
∵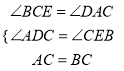 ,
,
∴△ADC≌△CEB(AAS).
(2)∵△ADC≌△CEB∴AD=CE,DC=EB.
又∵DE=DC+CE,∴DE=EB+AD=2+1=3.
∴△ABC的面积为: ![]() .
.


科目:初中数学 来源: 题型:
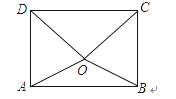
【题目】如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的有( )
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从下列不等式中选一个与x+2≥1组成不等式组,若要使该不等式组的解集为x≥﹣1,则可以选择的不等式是( )
A. x>﹣2 B. x>0 C. x<0 D. x<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要招聘电脑收银员,应聘者需通过计算机、语言和商品知识三项测试,小明的三项成绩(百分制)依次是70分,50分,80分,其中计算算机成绩占50%,语言成绩占30%,商品知识成绩占20%.则小明的最终成绩是( )
A.66分B.68分C.70分D.80分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的说法中,正确的个数是( )
①若a+b=0,则|a|=|b|
②若a<0,则|a|=﹣a
③若|a|=|b|,则a=b
④若a为有理数,则a2=(﹣a)2
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
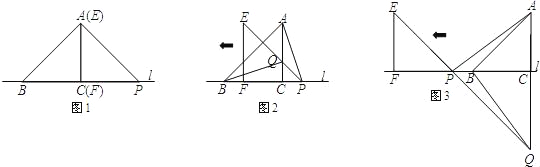
【题目】锐角为45°的直角三角形的两直角边长也相等,这样的三角形称为等腰直角三角形.我们常用的三角板中有一块就是这样的三角形,也可称它为等腰直角三角板.把两块全等的等腰直角三角板按如图1放置,其中边BC、FP均在直线l上,边EF与边AC重合.
(1)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;
(2)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com