
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.

科目:初中数学 来源: 题型:
【题目】氢原子的半径大约是0.000 0077m,将数据0.000 0077用科学记数法表示为( )
A.0.77×10﹣5
B.0.77×10﹣6
C.7.7×10﹣5
D.7.7×10﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AN⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4![]() 时,a= ,b= ;
时,a= ,b= ;
如图2,当∠PAB=30°,c=2时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3![]() ,AB=3,求AF的长.
,AB=3,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列性质中,菱形具有而矩形不一定具有的性质是( ).
A.对边平行且相等B.对角线互相平分
C.内角和等于外角和D.每一条对角线所在直线都是它的对称轴
查看答案和解析>>
科目:初中数学 来源: 题型:
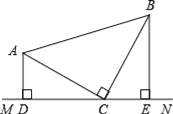
【题目】如图,在△ABC中∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)求证:△ADC≌△CEB;
(2)若AD=1,BE=2,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2﹣2x+3向上平移1个单位,平移后所得的抛物线的表达式为( )
A.y=x2﹣2x+4B.y=x2﹣2x+2C.y=x2﹣3x+3D.y=x2﹣x+3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com