
【题目】如图,一个商人要建一个矩形的仓库,仓库的两边是住房墙,另外两边用![]() 长的建筑材料围成,且仓库的面积为
长的建筑材料围成,且仓库的面积为![]() .
.

![]() 求这矩形仓库的长;
求这矩形仓库的长;
![]() 有规格为
有规格为![]() 和
和![]() (单位:
(单位:![]() )的地板砖单价分别为
)的地板砖单价分别为![]() 元/块和
元/块和![]() 元/块,若只选其中一种地板砖都恰好能铺满仓库的矩形地面(不计缝隙),用一种规格的地板砖费用较少?
元/块,若只选其中一种地板砖都恰好能铺满仓库的矩形地面(不计缝隙),用一种规格的地板砖费用较少?
【答案】(1)这矩形仓库的长是![]() (2)采用
(2)采用![]() 规格的地板砖费用较少
规格的地板砖费用较少
【解析】
(1)设矩形仓库的长为xm(10<x<20),则宽为(20-x)m,根据矩形仓库的面积为96m2,即可得出关于x的一元二次方程,解方程即可得出结论;
(2)根据费用=仓库面积÷单块地板砖的面积×地板砖的单价,分别求出铺两种规格地板砖各需的费用,比较后即可得出结论.
(1)设矩形仓库的长为xm(10<x<20),则宽为(20-x)m.
根据题意,得:x(20-x)=96,
整理,得;x2-20x+96=0,
解得:x1=12,x2=8(舍去),
答:这矩形仓库的长是12m.
(2)规格为0.80×0.80所需的费用:96÷(0.8×0.8)×55=8250(元);
规格为1.00×1.00所需的费用:96÷(1×1)×80=7680元.
∵8250>7680,
∴采用1.00×1.00规格的地板砖费用较少.


科目:初中数学 来源: 题型:
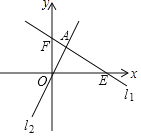
【题目】如图,在平面直角坐标系中,点E的坐标为(4,0),点F的坐标为(0,2),直线11经过点E和点F,直线l1与直线l2:y=2x相交于点A.
(1)求直线l1的表达式;
(2)求点A的坐标;
(3)求△AOE的面积;
(4)当点P是直线l1上的一个动点时,过点P作y轴的平行线PB交直线l2于点B,当线段PB=3时,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知矩形![]() 的边长
的边长![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一动点
边上的一动点![]() 不同于
不同于![]() 、
、![]() ,
,![]() 是
是![]() 边上的任意一点,连接
边上的任意一点,连接![]() 、
、![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() .设
.设![]() 的长为
的长为![]() ,则
,则![]() 的面积
的面积![]() 关于
关于![]() 的函数关系式是( )
的函数关系式是( )

A. ![]() B.
B. ![]()
C. .![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
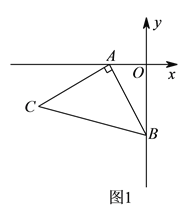
【题目】如图![]() ,
, ![]() ,
, ![]() ,以
,以![]() 点为顶点、
点为顶点、![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() .
.
(![]() )求
)求![]() 点的坐标.
点的坐标.
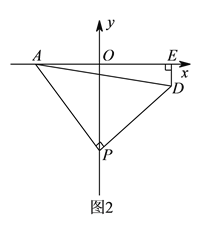
(![]() )如图
)如图![]() ,
, ![]() 为
为![]() 轴负半轴上一个动点,当
轴负半轴上一个动点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,以
轴负半轴向下运动时,以![]() 为顶点,
为顶点, ![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,求
点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,CD∥AB,点E是AC上一点,且∠ABE=∠CAD,延长BE交AD于点F.
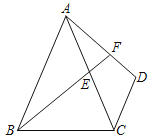
(1)求证:△ABE≌△CAD;
(2)如果∠ABC=65°,∠ABE=25°,求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 开始沿着边
开始沿着边![]() 向点
向点![]() 以
以![]() 的速度移动(不与点
的速度移动(不与点![]() 重合),动点
重合),动点![]() 从点
从点![]() 开始沿着边
开始沿着边![]() 向点
向点![]() 以
以![]() 的速度移动(不与点
的速度移动(不与点![]() 重合).若
重合).若![]() 、
、![]() 两点同时移动
两点同时移动![]() ;
;

![]() 当移动几秒时,
当移动几秒时,![]() 的面积为
的面积为![]() .
.
![]() 设四边形
设四边形![]() 的面积为
的面积为![]() ,当移动几秒时,四边形
,当移动几秒时,四边形![]() 的面积为
的面积为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在Rt△ABC中, ∠ACB=90°,AC=BC, D是线段AB上一点,连结CD,将线段CD绕点C 逆时针旋转90°得到线段CE,连结DE,BE.
(1)依题意补全图形;
(2)若![]() 用含
用含![]() 的代数式表示
的代数式表示![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、点B分别是y轴、x轴上两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;

(1)如图(1),已知C点的横坐标为-1,直接写出点A的坐标;
(2)如图(2), 当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
(3)如图(3), 若点A在x轴上,且A(-4,0),点B在y轴的正半轴上运动时,分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC,连结CD交y轴于点P,问当点B在y轴的正半轴上运动时,BP的长度是否变化?若变化请说明理由,若不变化,请求出BP的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com