
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 开始沿着边
开始沿着边![]() 向点
向点![]() 以
以![]() 的速度移动(不与点
的速度移动(不与点![]() 重合),动点
重合),动点![]() 从点
从点![]() 开始沿着边
开始沿着边![]() 向点
向点![]() 以
以![]() 的速度移动(不与点
的速度移动(不与点![]() 重合).若
重合).若![]() 、
、![]() 两点同时移动
两点同时移动![]() ;
;

![]() 当移动几秒时,
当移动几秒时,![]() 的面积为
的面积为![]() .
.
![]() 设四边形
设四边形![]() 的面积为
的面积为![]() ,当移动几秒时,四边形
,当移动几秒时,四边形![]() 的面积为
的面积为![]() ?
?
【答案】(1)32cm2(2)当移动![]() 秒时,四边形
秒时,四边形![]() 的面积为
的面积为![]()
【解析】
(1)找出运动时间为t秒时PB、BQ的长度,根据三角形的面积公式结合△BPQ的面积为32cm2,即可得出关于t的一元二次方程,解之即可得出结论;
(2)用△ABC的面积减去△BPQ的面积即可得出S,令其等于108即可得出关于t的一元二次方程,解之即可得出结论.
(1)运动时间为t秒时(0≤t<6),PB=AB-2t=12-2t,BQ=4t,
∴S△BPQ=![]() PBBQ=24t-4t2=32,
PBBQ=24t-4t2=32,
解得:t1=2,t2=4.
答:当移动2秒或4秒时,△BPQ的面积为32cm2.
(2)S=S△ABC-S△BPQ=![]() ABBC-(24t-4t2)=4t2-24t+144=108,
ABBC-(24t-4t2)=4t2-24t+144=108,
解得:t=3.
答:当移动3秒时,四边形APQC的面积为108cm2.


 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
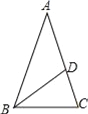
【题目】如图,在△ABC中,AB=AC=1,BC=![]() ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与ACCD的大小关系;
(2)求∠ABD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市开展的环境创优活动中,某居民小区要在一块靠墙(墙长![]() 米)的空地上修建一个矩形花园
米)的空地上修建一个矩形花园![]() ,花园的一边靠墙,另三边用总长为
,花园的一边靠墙,另三边用总长为![]() 的栅栏围成,若设花园平行于墙的一边长为
的栅栏围成,若设花园平行于墙的一边长为![]() ,花园的面积为
,花园的面积为![]() .
.
![]() 求
求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 满足条件的花园面积能达到
满足条件的花园面积能达到![]() 吗?若能,求出此时
吗?若能,求出此时![]() 的值,若不能,说明理由;
的值,若不能,说明理由;
![]() 根据
根据![]() 中求得的函数关系式,判断当
中求得的函数关系式,判断当![]() 取何值时,花园的面积最大,最大面积是多少?
取何值时,花园的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个商人要建一个矩形的仓库,仓库的两边是住房墙,另外两边用![]() 长的建筑材料围成,且仓库的面积为
长的建筑材料围成,且仓库的面积为![]() .
.

![]() 求这矩形仓库的长;
求这矩形仓库的长;
![]() 有规格为
有规格为![]() 和
和![]() (单位:
(单位:![]() )的地板砖单价分别为
)的地板砖单价分别为![]() 元/块和
元/块和![]() 元/块,若只选其中一种地板砖都恰好能铺满仓库的矩形地面(不计缝隙),用一种规格的地板砖费用较少?
元/块,若只选其中一种地板砖都恰好能铺满仓库的矩形地面(不计缝隙),用一种规格的地板砖费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰三角形△ABC,BC边上的高恰好等于BC边长的一半,则∠BAC的度数是( )
A.75°B.90°或75°C.90°或 75°或15°D.75°或15°或60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com